I have a tensor a with shape (100,140,140) which is actually a batch (size 100) of matrices of size (140x140). You can assume these matrices are actually vectors with 140x140 = 19600 components.
I also have a function myfunc(a, b, c, d) where b, c, d are some constant tensors. myfunc() outputs a batch of scalers. Now I want to find the gradient of myfunc(a, b, c, d) with respect to the vectors in tensor a using Finite Difference Method:
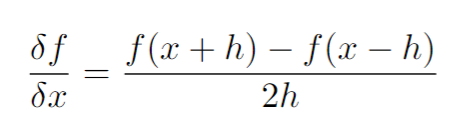
What I am trying to do right now is something like this:
grad_a = torch.empty_like(a)
for i in range(a.shape[1]):
for j in range(a.shape[2]):
a[:,i,j] += h #h is the step size
out1 = myfunc(a, b, c, d)
a[:,i,j] -= 2*h
out2 = myfunc(a, b, c, d)
grad_a[:,i,j] = (out1 - out2)/(2*h)
a[:,i,j] += h #resetting the value to original
I am fairly new to pytorch and don’t really know how to do these avoiding a loop. For loop is really slow on this and may not even finish on my system with larger tensors. Is there any torch functionality to do these efficiently without a loop? I have found this FDM Library but I don’t know how to use the gradient method from that library on functions with more than 1 parameter.
Any help is appreciated. Thank you!