Hello PyTorch users,
I am trying to solve Exercise 4 from section 7.6 of the Dive into Deep Learning book. While solving it, however, I get training loss NaN and 0.1 for training and test accuracy. The exercise in question goes as follows:
In subsequent versions of ResNet, the authors changed the “convolution, batch normalization, and activation” structure to the “batch normalization, activation, and convolution” structure. Make this improvement yourself. See Figure 1 in [He et al., 2016b] for details.
So, what I did was changed the original version of the Residual class from this:
class Residual(nn.Module): #@save
"""The Residual block of ResNet."""
def __init__(self, input_channels, num_channels, use_1x1conv=False,
strides=1):
super().__init__()
self.conv1 = nn.Conv2d(input_channels, num_channels, kernel_size=3,
padding=1, stride=strides)
self.conv2 = nn.Conv2d(num_channels, num_channels, kernel_size=3,
padding=1)
if use_1x1conv:
self.conv3 = nn.Conv2d(input_channels, num_channels,
kernel_size=1, stride=strides)
else:
self.conv3 = None
self.bn1 = nn.BatchNorm2d(num_channels)
self.bn2 = nn.BatchNorm2d(num_channels)
def forward(self, X):
Y = F.relu(self.bn1(self.conv1(X)))
Y = self.bn2(self.conv2(Y))
if self.conv3:
X = self.conv3(X)
Y += X
return F.relu(Y)
to this:
class Residual(nn.Module): #@save
"""The Residual block of ResNet."""
def __init__(self, input_channels, num_channels, use_1x1conv=False,
strides=1):
super().__init__()
self.conv1 = nn.Conv2d(input_channels, num_channels, kernel_size=3,
padding=1, stride=strides)
self.conv2 = nn.Conv2d(num_channels, num_channels, kernel_size=3,
padding=1)
if use_1x1conv:
self.conv3 = nn.Conv2d(input_channels, num_channels,
kernel_size=1, stride=strides)
else:
self.conv3 = None
#self.bn1 = nn.BatchNorm2d(num_channels)
self.bn1 = nn.BatchNorm2d(input_channels)
self.bn2 = nn.BatchNorm2d(num_channels)
def forward(self, X):
Y = self.conv1(F.relu(self.bn1(X)))
Y = F.relu(self.bn2(Y))
if self.conv3:
X = self.conv3(X)
Y += X
return self.conv2(Y)
The rest of the code is the same as in the book (I only modified the Residual block, so the error must be there somewhere). I state the other code below, for the sake of completeness:
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
nn.BatchNorm2d(64), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
def resnet_block(input_channels, num_channels, num_residuals,
first_block=False):
blk = []
for i in range(num_residuals):
if i == 0 and not first_block:
blk.append(
Residual(input_channels, num_channels, use_1x1conv=True,
strides=2))
else:
blk.append(Residual(num_channels, num_channels))
return blk
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))
net = nn.Sequential(b1, b2, b3, b4, b5, nn.AdaptiveAvgPool2d((1, 1)),
nn.Flatten(), nn.Linear(512, 10))
X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
X = layer(X)
print(layer.__class__.__name__, 'output shape:\t', X.shape)
|Sequential output shape:| torch.Size([1, 64, 56, 56])|
|---|---|
|Sequential output shape:| torch.Size([1, 64, 56, 56])|
|Sequential output shape:| torch.Size([1, 128, 28, 28])|
|Sequential output shape:| torch.Size([1, 256, 14, 14])|
|Sequential output shape:| torch.Size([1, 512, 7, 7])|
|AdaptiveAvgPool2d output shape:| torch.Size([1, 512, 1, 1])|
|Flatten output shape:| torch.Size([1, 512])|
|Linear output shape:| torch.Size([1, 10])|
lr, num_epochs, batch_size = 0.05, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
The training code (again, from the book; not modified by me) is:
def train_ch6(net, train_iter, test_iter, num_epochs, lr, device):
"""Train a model with a GPU (defined in Chapter 6)."""
net.initialize(force_reinit=True, ctx=device, init=init.Xavier())
loss = gluon.loss.SoftmaxCrossEntropyLoss()
trainer = gluon.Trainer(net.collect_params(), 'sgd',
{'learning_rate': lr})
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
legend=['train loss', 'train acc', 'test acc'])
timer, num_batches = d2l.Timer(), len(train_iter)
for epoch in range(num_epochs):
# Sum of training loss, sum of training accuracy, no. of examples
metric = d2l.Accumulator(3)
for i, (X, y) in enumerate(train_iter):
timer.start()
# Here is the major difference from `d2l.train_epoch_ch3`
X, y = X.as_in_ctx(device), y.as_in_ctx(device)
with autograd.record():
y_hat = net(X)
l = loss(y_hat, y)
l.backward()
trainer.step(X.shape[0])
metric.add(l.sum(), d2l.accuracy(y_hat, y), X.shape[0])
timer.stop()
train_l = metric[0] / metric[2]
train_acc = metric[1] / metric[2]
if (i + 1) % (num_batches // 5) == 0 or i == num_batches - 1:
animator.add(epoch + (i + 1) / num_batches,
(train_l, train_acc, None))
test_acc = evaluate_accuracy_gpu(net, test_iter)
animator.add(epoch + 1, (None, None, test_acc))
print(f'loss {train_l:.3f}, train acc {train_acc:.3f}, '
f'test acc {test_acc:.3f}')
print(f'{metric[2] * num_epochs / timer.sum():.1f} examples/sec '
f'on {str(device)}')
with evaluate_accuracy_gpu being defined as follows:
def evaluate_accuracy_gpu(net, data_iter, device=None): #@save
"""Compute the accuracy for a model on a dataset using a GPU."""
if not device: # Query the first device where the first parameter is on
device = list(net.collect_params().values())[0].list_ctx()[0]
# No. of correct predictions, no. of predictions
metric = d2l.Accumulator(2)
for X, y in data_iter:
X, y = X.as_in_ctx(device), y.as_in_ctx(device)
metric.add(d2l.accuracy(net(X), y), y.size)
return metric[0] / metric[1]
Here is the training graph:
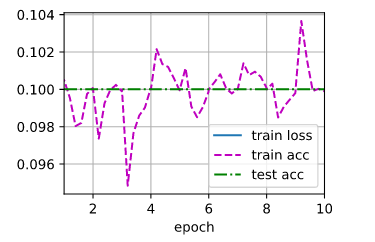
Some additional information:
The dataset is fashion MNIST. Training loss is NaN after 10 epochs. I don’t measure the test loss. I used a function for loading the fashion MNIST dataset into memory from the Dive into Deep Learning book and I believe it keeps the same distribution of classes as in the dataset (it is stratified).
Do you see what is the issue?
Thank you in advance!