Hi! After reading the material below, I have a question.
According to ch2 useful identities (5), (6) in the pdf above, the formula is defined as follows.
(5) Matrix times column vector with respect to the matrix
(6) Row vector time matrix with respect to the matrix
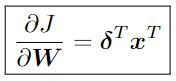
I was wondering if this would actually be true, so I implemented it with pytorch
import random
import numpy as np
import torch
def set_seed(seed: int = 42):
"""Seed fixer (random, numpy, torch)
Args:
seed (:obj:`int`): The seed to set.
"""
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed) # if use multi-GPU
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
set_seed()
# (5) column vector case
x = torch.randn(5, 1).requires_grad_()
W = torch.randn(3, 5).requires_grad_()
y = W @ x
torch.isclose(
torch.ones_like(y) @ x.T, # delta * x^T
torch.autograd.grad(y, W, torch.ones_like(y), retain_graph=True)[0]
)
# (6) row vector case
x = torch.randn(1, 2).requires_grad_()
f = torch.nn.Linear(2, 3, bias=False).requires_grad_()
y = f(x)
torch.autograd.backward(y, torch.ones_like(y), retain_graph=True)
assert torch.isclose(
x.T @ torch.ones_like(y), # x^T * delta
# Since
nn.Linear in torch stores weights as transpose
torch.autograd.grad(y, f.weight, torch.ones_like(y), retain_graph=True)[0].T
)
In my results, the row vector case was the same as the pdf, but the column vector case was different.
And even when I understood it as a formula, I did not understand it.
In (5), delta means \frac{\partial J}{\partial z}, which will be a column vector. In order to perform outer product, it is necessary to calculate column vector X row vector, but it is strange to take transpose.
Is the formula wrong? Or is the implementation wrong?