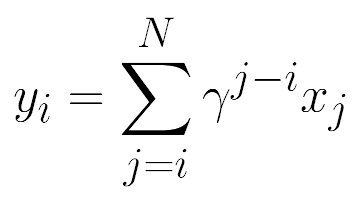Cumulative sum with a discount factor

1

I’m looking for a algorithm to calculate cumulative sum with decay factor for a tensor. With the formula:
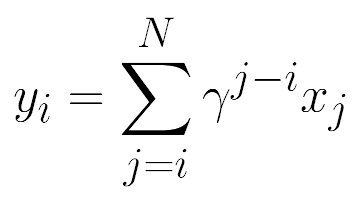
image
I’ve tried several methods, but all them make some errors:

  1. GitHub - toshas/torch-discounted-cumsum: Fast Discounted Cumulative Sums in PyTorch This library seems to work but causes a series of errors about CUDA version.
  2. Cumulative sum with decay factor - PyTorch Forums Algorithm here has precision issues and results in nan value while calculating loss.
  3. Inplace operations causes error while using autograd.

Many thanks for your reply and help : D.

2

Hi @jiyuechenxing,

Couldn’t you just compute the discount factor as an array and then element-wise multiplication it to the x? Then use torch.cumsum as usual?

Also, are the indicies correct with your equation? If j=i then surely \gamma^{j-1} equals 1 by definition?

3

Yes, that’s the case.
Now I realize the function with the method in Cumulative sum with decay factor - PyTorch Forums. I add small bias (1e-6) to the denominator to avoid Tensor/0. It indeed works but now I just don’t know how it would affect my model.
Thank you again for your reply. :smiling_face:

4

If you want to skip over a given element to avoid a divide-by-zero error, you could always just wrap the previous comment in a torch.where statement.

So, if the denominator is zero you just multiple by 1 and else use the array value as normal. This should remove the 1e-6 bias that you added to your calculation.