Tl;dr Porting between implementations like CPU, CUDA does not provide consistent results
I am investigating various implementations of different layers as I try to port a model, and I observed significant deviation between different implementations. While torch defaults to torch.float for most things which is supposed to be float32 implementations, trying to use the raw data seems almost impossible for functions of reasonable sizes.
For reference here are my observations of a linear layer.
First of all I look at an explicit full connected implementation vs F.linear
@torch.no_grad()
def test():
in_chan = 2048
out_chan = 512
in_len = 32
W = torch.randn(out_chan, in_chan)
B = torch.randn(out_chan)
x = torch.randn(in_len, in_chan)
y_t1 = (x @ W.T + B)
y_t2 = F.linear(x, W, B)
print((y_t1 - y_t2).abs().sum()) # tensor(0.0291)
print(torch.allclose(y_t1, y_t2)) # False
test()
While the implementation on CUDA by itself seem fine, comparing it with CPU shows even more errors
@torch.no_grad()
def test():
in_chan = 2048
out_chan = 512
in_len = 32
W = torch.randn(out_chan, in_chan).cuda()
B = torch.randn(out_chan).cuda()
x = torch.randn(in_len, in_chan).cuda()
y_t1_cuda = (x @ W.T + B)
y_t2_cuda = F.linear(x, W, B)
print((y_t1_cuda - y_t2_cuda).abs().sum()) # 0
print(torch.allclose(y_t1_cuda, y_t2_cuda)) # True
W = W.cpu()
B = B.cpu()
x = x.cpu()
y_t1_cpu = (x @ W.T + B)
y_t2_cpu = F.linear(x, W, B)
print((y_t1_cpu - y_t2_cpu).abs().sum()) # 0.0295
print(torch.allclose(y_t1_cpu, y_t2_cpu)) # False
print((y_t1_cpu - y_t1_cuda.cpu()).abs().sum()) # 0.1881
test()
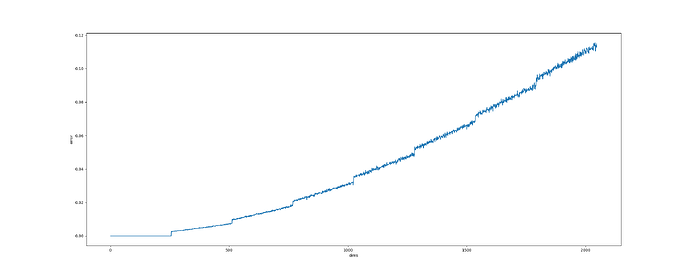
on further testing I can see the errors accumulate with increasing dimensions
@torch.no_grad()
def test():
dims = np.arange(1, 2048)
y = []
for dim in dims:
in_chan = out_chan = dim
in_len = 32
W = torch.randn(out_chan, in_chan)
B = torch.randn(out_chan)
x = torch.randn(in_len, in_chan)
y_t1 = (x @ W.T + B)
y_t2 = F.linear(x, W, B)
y += [(y_t1 - y_t2).abs().sum()]
y = torch.tensor(y).numpy()
plt.figure(figsize=(25, 10))
plt.plot(dims, y)
plt.ylabel('error')
plt.xlabel('dims')
curdir = Path(__file__).resolve().parent
plt.savefig(f'{curdir}/errors.png')
test()
I reached this problem while trying to port implementation to numpy as a sanity check where I first noticed these deviations
@torch.no_grad()
def test():
def with_type(t):
in_chan = 2048
out_chan = 512
in_len = 32
W = np.random.randn(out_chan, in_chan).astype(t)
B = np.random.randn(out_chan).astype(t)
x = np.random.randn(in_len, in_chan).astype(t)
y_t1 = (x @ W.T + B)
y_t2 = F.linear(
torch.tensor(x),
torch.tensor(W),
torch.tensor(B)
).numpy().astype(t)
print(np.sum(np.abs(y_t1 - y_t2)))
with_type('float32') # 0.027533546
with_type('float64') # 5.6747252730193765e-11
test()
while the errors in float64 implementations are smaller, I suspect for much larger model they would accumulate to significant levels as well.