Different results when manually optimizing a network's parameters

autograd
1

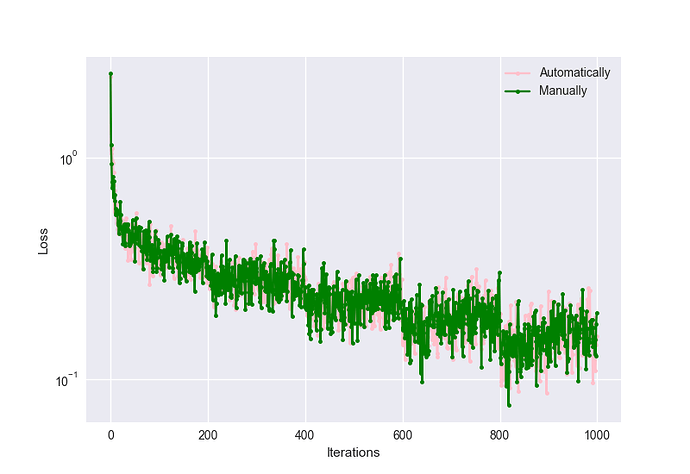
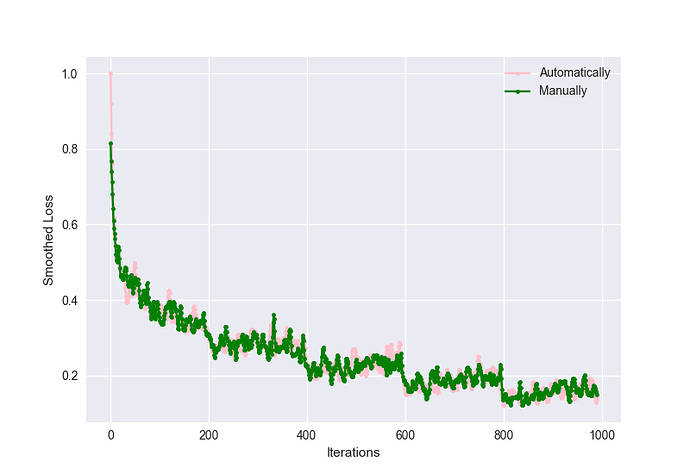
I’ve been playing around with the autograd engine, attempting to “manually” update a network’s parameters via the autograd mechanism, replicating SGD. However, in doing so, I’ve got different results compared to the automatic/conventional way of updating a network’s parameters (using opt.step()). I’ve had the following settings to ensure reproducibility when running the same network using the different updating schemes:

device = torch.device('cuda')
torch.cuda.empty_cache()
torch.manual_seed(0)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
np.random.seed(0)

The network used was a simple multi-layer FFN (MNIST classification):

class Model(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Sequential(nn.Linear(784, 1440, bias=False), nn.BatchNorm1d(1440), nn.ReLU())
        self.fc2 = nn.Sequential(nn.Linear(1440, 1440, bias=False), nn.BatchNorm1d(1440), nn.ReLU())
        self.fc3 = nn.Sequential(nn.Linear(1440, 784, bias=False), nn.BatchNorm1d(784), nn.ReLU())
        self.fc4 = nn.Sequential(nn.Linear(784, 784, bias=False), nn.BatchNorm1d(784), nn.ReLU())
        self.fc5 = nn.Linear(784, 10)

    def forward(self, x):
        return nn.Sequential(*list(self.children()))(x)

Updating the network using the “manual” way was done in the following manner:

m2 = Model().to(device)
for e in trange(epochs):
    for x, y in train_loader:
        x, y = x.to(device, non_blocking=True), y.to(device, non_blocking=True)
        loss = F.cross_entropy(m2(x), y)
        grad = torch.autograd.grad(loss, m2.parameters())
        for p, g in zip(m2.parameters(), grad):
            p.data -= LR * g

While updating the network using the “automatic/conventional” way was as follows:

m1 = Model().to(device)
opt = torch.optim.SGD(m1.parameters(), lr=LR)
for e in trange(epochs):
    for x, y in train_loader:
        x, y = x.to(device, non_blocking=True), y.to(device, non_blocking=True)
        loss = F.cross_entropy(m1(x), y)
        loss.backward()
        opt.step()
        opt.zero_grad()

The learning rates and epochs used are the same in both cases.

Here is a visualization of the results I got:

fig1
fig1800×550 47.7 KB

Figure_2
Figure_2800×550 35.2 KB

While the accuracies were:

Accuracy (Automatic): 88.0%
Accuracy (Manual): 86.7%

Can someone explain to me why these differences arise? Is there something extra going on behind the hood?

2

Based on the posted images it looks as if the very first loss value is already different before the parameter update was performed. Could you compare the initial parameters as well as the input and loss value before comparing the parameter updates?

1 Like
4

Thanks for the response; yes, you’re totally right. After comparing the initial state of the parameters of the two models, it turned out that they differed in every nn.Linear() weight initialization but had the same weight and bias initializations for the BatchNorms (nn.BatchNorm1d()).

I guess the question now is how to enforce the same weight initialization for all the nn.Linear() modules in both models?

5

You could either load the state_dict from one model to the other or seed the code carefully before initializing the models and make sure the order of calls into pseudorandom number generator is the same.

1 Like
6

Yeah, that sounds like a great idea; however, I’m getting this weird behavior now where after I did the following:

m1 = Model().to(device)
m2 = Model().to(device)
m2.load_state_dict(m1.state_dict())

And then manually checked whether the initial state of the parameters in both models was equivalent (which it was), the initial loss value was still different (and throughout)! Not only that, but the Accuracy (Automatic) went to 88.21% from 88.0%. Somehow loading m1's state dictionary into m2 affected m1?

I even tried the following:

m1 = Model().to(device)
m2 = deepcopy(m1)

Yet again, manually checking all the parameters showed they were indeed equivalent throughout the whole network. However, I’m still getting different results (though the Accuracy (Automatic) this time matches the original one (i.e., 88.0%)).

7

If the parameters are equal but the results still differ, your input data is either not the same or your model is applying some random operations (e.g. dropout) which can be disabled via calling model.eval().

1 Like
8

After forcing the to inputs to be exactly the same, and in the exact same order sequentially (disabled shuffling for extra measure), I finally started getting same initial loss evolution, though they slightly differ towards the end and give slightly different results, but at least it’s much better than before. Thanks a lot!