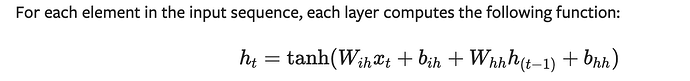Dimensionslity in RNN

#1

For instance I have this rnn:

rnn = torch.nn.RNN(2, 2, 1, batch_first = True)

and I have input of:
x = torch.tensor([[[1,1], [2,2], [3,3]], [[2,2], [3,3], [4,4]], [[4,4], [5,5], [6,6]]])
My model shows that it have this type of parameters:

weight_ih_l0 tensor([[-0.1641, -0.6958],
        [ 0.1889,  0.4084]])
weight_hh_l0 tensor([[ 0.0063, -0.5073],
        [-0.2890, -0.5403]])
bias_ih_l0 tensor([-0.0039, -0.2850])
bias_hh_l0 tensor([ 0.5279, -0.1149])

If hidden is initialized as none my output will be like:

hidden = None 
out, hidden = rnn(x.float(), hidden)
out
tensor([[[-0.3238,  0.1948],
         [-0.8609,  0.6544],
         [-0.9835,  0.8584]],

        [[-0.8324,  0.6611],
         [-0.9836,  0.8553],
         [-0.9976,  0.9480]],

        [[-0.9941,  0.9633],
         [-0.9996,  0.9821],
         [-0.9999,  0.9945]]]

So this RNN hidden state have this formula:
h_t = tanh(w_{ih} * x_t + b_{ih} + w_{hh} * h_{(t-1)} + b_{hh})
but w_{ih} will have shape 2X2 and x_t will have shape 1X2 (for instance first input [1,1]), how then they multiple and work? Or is it work differently in pytorch?
I am asking this question because I tried to recreate this in numpy, but this call error due to inappropriate dimensions in this part, which is right from lin. alg. point of view.

h_t = numpy.tanh(hh@hidden + ih@numpy.matrix([1,1]) + bias_ih + bias_hh)
#2

When I tried recreated in numpy I just copied for instance like this:

weight_ih_l0 tensor([[-0.1641, -0.6958],
       [ 0.1889,  0.4084]])

then
ih = numpy.matrix([[-0.1641, -0.6958],
       [ 0.1889,  0.4084]])

bias_ih = ([-0.0039, -0.2850])
and so on

But when I reshaped my bias and my input like this:

bias_ih = numpy.matrix([[-0.0039],  [-0.2850])
(and another bias)
h_t = numpy.tanh(hh@hidden + ih@numpy.matrix([[1],[1]]) + bias_ih + bias_hh)

it is started to work correctly and match pytorch outputs, so is there auto-reshaper of some kind or pytorch have some kind of different printed shape(sorry for reinventing words :/)?

#4

Okay aldeka, starting from the creation of your instance, it means rnn = torch.nn.RNN(2, 2, 1, batch_first = True), starting from the left, it means that that your input size =2 (meaning each sequence has to values), 2 meaning that each of your input sequence will have an output that 2 values long and 1 means you just have 1 layer in your network. So the dimension of your input is [3,3,2] starting from the right 2 = feature size (meaning each of your input sequences has 2 features), 3 = number of sequences in each batch, 3 = batch_size(and each batch has 3 sequences which are all 2 vectors long). Just for your information each batch will have its hidden vector. So lets try and calculate the output of the the first input of the first batch using the formula from the pytorch documentation.

Screen Shot 2020-03-23 at 16.19.05
Screen Shot 2020-03-23 at 16.19.051250×148 10.8 KB

W_{ih} = torch.tensor([[ 0.0063, -0.5073], [-0.2890, -0.5403]])

  • The dimension is [2,2]. It has 2 rows because the output_size is 2 and it has 2 columns because the every input has has 2 features. So in general, the dimension of the weight of an input is [output_size, input_feature_size].

X{t} = torch.tensor([[[1, 1]]])

  • This is the dimension is [1,1,2] , but we would have to reshape it to [2,1] to obey the matrix dot rule. we can reshape by first saying x= x.squeeze(0) and saying x = x.t() , the latter one is to get the transpose.
  • Finally it will become tensor([[1], [1]])

b{ih} = torch.tensor([-0.0039, -0.2850])

  • The dimension of the bias of the input is just [2], so you would have to reshape it to [2,1] by saying b = b.reshape(2,1).

W{hh} = torch.tensor([[ 0.0063, -0.5073], [-0.2890, -0.5403]])

  • The dimension of this is [2,2], this is always a square matrix. And in general its dimension is [hidden_size,hidden_size]

h{t_1} = In your case you did not create the hidden yourself but the dimension of hidden is always [number_of_layers,batch_size, hidden_size]

  • By the way each batch of input will have its own hidden vector and each hidden vector size will depend on the number of output features you have. In your case, instead of saying the hidden to be none , you can create it as hidden = torch.rand(1,3,2). Starting from the left , 1 = number of layers, 3 = number of batches from input , and lastly each of the hidden vector of each batch is has a size of 2.
  • So lets assume it is torch.tensor([[[0.8888, 0.8303], [0.9467, 0.4717], [0.1862, 0.6796]]]) , Meaning the hidden [0.8888, 0.8303] for the first batch , the hidden [0.9467, 0.4717] is for the second batch and the hidden [0.1862, 0.6796] is for the 3rd batch.

b{hh} = torch.tensor([ 0.5279, -0.1149])

  • The dimension of the bias of the hidden is just [2], so you would have to reshape it to [2,1] by using this code b = b.reshape(2,1)

Finally, using the above formula, the dimension would be

  • ``( [2,2] * [2,1] )+ [2,1] + ([ 2,2 ] * [2,1] )+ [2,1])

  • ( torch.tensor([[ 0.0063, -0.5073], [-0.2890, -0.5403]]) * torch.tensor([[1], [1]]) ). —> which is w_{ih} * x . Lets call this a1

  • torch.tensor([-0.0039, -0.2850]) – which is b{ih} – call this a2

  • torch.tensor(torch.tensor([[ 0.0063, -0.5073], [-0.2890, -0.5403]]) *[0.8888, 0.8303] ) --> w{hh}* h{t-1} – call this a3

  • torch.tensor([ 0.5279, -0.1149]) --> b{hh} --call this a3

FINAL RESULT IS a1+a2+a3+a4