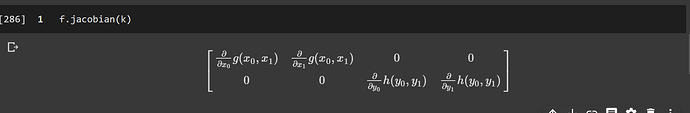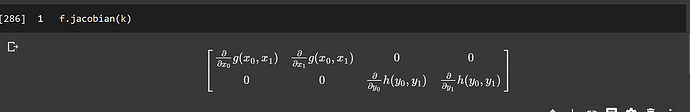Doubt regarding shape after Jacobian

[vainaijr]

when I apply Jacobian in PyTorch autograd (torch==1.5.0), it gives me three dimensional output.
for example,

def exp_reducer(x):
    return (x**2).sum(dim=1)
inputs = torch.rand(2, 2)
torch.autograd.functional.jacobian(exp_reducer, inputs)

tensor([[[0.3296, 0.9791],
         [0.0000, 0.0000]],

        [[0.0000, 0.0000],
         [1.6706, 0.7365]]])

and

torch.autograd.functional.jacobian(exp_reducer, inputs).shape

(2,2,2)

but I get a 2 dimensional output when using sympy,

x0, y0, x1, y1= sympy.symbols('x0, y0, x1, y1')
f = Matrix([Function('g')(x0, x1), Function('h')(y0, y1)])
k = Matrix([[x0, x1, y0, y1]])
f.jacobian(k)

then it give me, this,

should the shape after applying Jacobian be 2d or 3d?

[albanD]

Hi,

Yes we follow a slightly different semantic.
The usual definition for multivariate functions is given a 1D input and 1D output, you end up with as 2D Jacobian.

What sympy is doing here is to linearize the inputs from a (2, 2) Tensor into a (4,) Tensor. And so the Jacobian is (2, 4).

Because we usually allow multiple Tensors, people very often multiple dimensions and linearizing the Tensors can be confusing if you don’t know how they are layed out in memory, we made a different choice here (similar to what tensorflow or jax are doing).
Here we don’t linearize Tensors and so you can index your Jacobian the same way you would index your original Tensor.

[vainaijr]

Would it be a good idea to add the symbolic representation to docs?
When computing hessian, I get same dimension confusion,
for example,

def pow_adder_reducer(x, y):
  print('x: ', x, 'y: ', y)
  return (2 * x.pow(2) + 3 * y.pow(2)).sum()
inputs = (torch.rand(2), torch.rand(2))
torch.autograd.functional.hessian(pow_adder_reducer, inputs)

PyTorch gives,

x:  tensor([0.4406, 0.9028], grad_fn=<ViewBackward>) y:  tensor([0.8790, 0.7052], grad_fn=<ViewBackward>)
((tensor([[4., 0.],
          [0., 4.]]), tensor([[0., 0.],
          [0., 0.]])), (tensor([[0., 0.],
          [0., 0.]]), tensor([[6., 0.],
          [0., 6.]])))

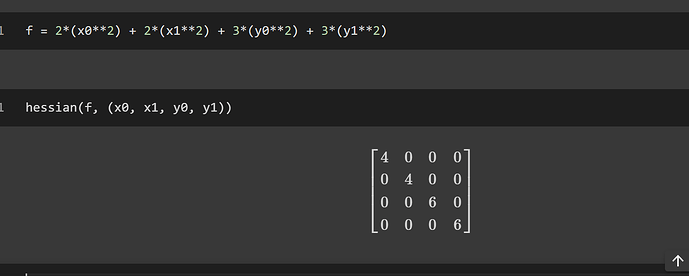
from sympy I get,

is it doing something like,

f1 = 2*(x0**2) + 2*(x1**2)
f2 = 3*(y0**3) + 3*(y1**3)

hessian(f1, (x0, x1))

hessian(f1, (y0, y1))

hessian(f2, (x0, x1))

hessian(f2, (y0, y1))

that results in four 2x2 matrices.

[albanD]

Yes, this is a similar argument. The indexing is interleaved as output tensor, input tensor, output dim, input dim.
You can check the discussion we had about this on the original issue here: Add high level autograd functions · Issue #30632 · pytorch/pytorch · GitHub

Would it be a good idea to add the symbolic representation to docs?

Definitely open to suggestions to improve the doc !
What do you mean here by “symbolic representation”? Could you give an example?

[vainaijr]

Like this one,

and this one,

like this symbolic representation added to docs, this makes it a bit easier to understand when we input >1d tensor.

[albanD]

Thanks, I added it to the issue to work on doc improvements here: https://github.com/pytorch/pytorch/issues/34998
Feel free to post there if you have more ideas !