I am new to pytorch and trying to use it to solve an underdetermined problem where I have a limited number of samples of an FFT. For now I am using the entire FFT and just a squared error loss.
My output looks like a rightside-up image superimposed on an upside-down image:
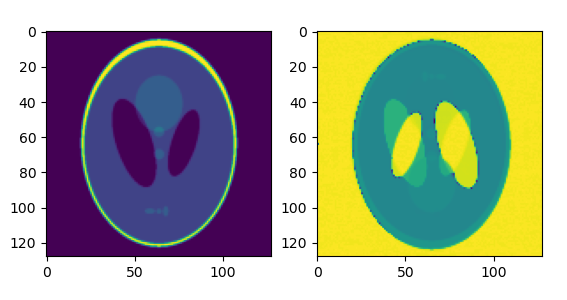
I think this means I am losing the imaginary values somewhere. I verified that all the operations (subtraction, squaring, summing) are behaving as I expect in the loss calculation. What could be causing this?
Here is my code:
import torch
import numpy as np
import matplotlib.pyplot as plt
from skimage.data import shepp_logan_phantom
from skimage.transform import resize
imsize = 128
image = resize(shepp_logan_phantom(),(imsize,imsize))
fftimage = np.fft.fft2(image)
x = torch.zeros((imsize,imsize)) # guess
x.requires_grad = True
optimizer = torch.optim.Adam([x], lr=5e-4)
data = torch.from_numpy(fftimage)
losses = []
def loss(x):
fftx = torch.fft.fft2(x)
loss = (data - fftx).pow(2).sum()
loss = loss.real.pow(2) + loss.imag.pow(2)
return loss
itera = 10000
for i in range(itera):
current_loss = loss(x)
optimizer.zero_grad()
current_loss.backward()
optimizer.step()
losses.append(current_loss)
reconstruction = x.detach().numpy()
fig1,ax1 = plt.subplots(1,1)
ax1.plot(losses)
ax1.set_yscale("log")
ax1.set_ylabel("loss")
ax1.set_xlabel("iterations")
fig,ax = plt.subplots(1,2)
ax[0].imshow(image)
ax[1].imshow(np.abs(reconstruction))