Hi everyone,
I have recently started working with neural nets and with pytorch, and I am trying to implement a Gumbel softmax VAE (based on the code here) to solve the following task:
- Encode a one-hot array with length 10. Latent space has dimension 10, too.
- Send a one-hot vector with length 10 to the decoder.
- Decode
I would have expected that it is a simple task for the network to learn to reconstruct the input perfectly, by simply copying the input vector. There is no bottleneck because all the hidden layers are also as large as the input. And yet, almost always the network ends up in some local minimum, where multiple input vectors receive the same encoding.
Here is the code for the Gumbel part:
import torch
import torch.nn.functional as F
from torch import nn, optim
import numpy as np
def sample_gumbel(shape, eps=1e-20):
"""
Parameters
----------
shape: tuple of ints
The dimension of the samples to take.
Returns
-------
Float tensor
Each element in the tensor is a sample from a Gumbel(0,1) distribution.
"""
# sample from a Gumbel(0,1) distribution can be obtained by sampling U from a Uniform(0,1)
# and then doing -log(-log(U))
U = torch.rand(shape)
return -torch.log(-torch.log(U + eps) + eps)
def gumbel_softmax_sample(logits, temperature):
"""
Takes a sample from a Gumbel distribution using the reparameterization trick.
Uses equation 2 in https://arxiv.org/pdf/1611.01144.pdf
Parameters
----------
logits: array
Class logprobabilities
temperature: float
Parameter of softmax
Returns
-------
Float tensor
An array containing a softmax version of samples from the Gumbel distribution.
"""
y = logits + sample_gumbel(logits.size())
# F.softmax applies a softmax function to a vector, which approximates an argmax function + one-hot
return F.softmax(y / temperature, dim=-1)
def gumbel_softmax(logits, temperature):
"""
Parameters
----------
logits: array
Shape (# instance, # classes). Contains the log-probabilities of each class for each instance
temperature: float
See gumbel_softmax_sample
Returns
-------
tensor
Every row is a one-hot vector.
"""
y = gumbel_softmax_sample(logits, temperature)
# find the argmax of each gumbel sample, for each row of logits
ind = y.argmax(dim=-1)
# create an array where each row is a one-hot vector for the respective index in ind
y_hard = torch.zeros_like(y)
y_hard.scatter_(1, ind.view(-1, 1), 1)
# detach the samples from the gradient calculation.
# Not sure why it was written this way!
y_hard = (y_hard - y).detach() + y
return y_hard
And here is the model itself:
class VAE_gumbel(nn.Module):
def __init__(self, temp, n_objects, n_signals):
self.n_objects, self.n_signals = n_objects, n_signals
super(VAE_gumbel, self).__init__()
# encoder layers
self.fc1 = nn.Linear(n_objects, 10)
self.fc2 = nn.Linear(10, 10)
self.fc3 = nn.Linear(10, n_signals)
# decoder layers
self.fc4 = nn.Linear(n_signals, 10)
self.fc5 = nn.Linear(10, 10)
self.fc6 = nn.Linear(10, n_objects)
# non linear transformations
self.relu = nn.ReLU()
self.sigmoid = nn.Sigmoid()
def encode(self, x):
x = self.relu(self.fc1(x))
x = self.relu(self.fc2(x))
return self.relu(self.fc3(x))
def decode(self, x):
x = self.relu(self.fc4(x))
x = self.relu(self.fc5(x))
# outputs a vector of probabilities
return F.softmax(self.fc6(x), dim=-1)
def probs_signals(self, x):
return F.softmax(self.encode(x), dim=-1)
@property
def language(self):
input_onehots = torch.eye(self.n_signals)
probs_signals = self.probs_signals(input_onehots).detach().numpy()
return probs_signals
def forward(self, x, temp):
# finds the vector of parameters to transform into logprobabilities
q = self.encode(x)
# these should be logprobabilities, because the gumbel_softmax distribution expects logprobabilities
q_logprobs = F.log_softmax(q, dim=-1)
z = gumbel_softmax(q_logprobs, temp)
return self.decode(z), F.softmax(q, dim=-1)
Finally, the loss function and the function to run:
def loss_function(recon_x, x, qy):
"""
The variational prior is a categorical distribution with uniform probabilities.
Reconstruction + KL divergence losses summed over all elements and batch
"""
BCE = F.binary_cross_entropy(recon_x, x, size_average=False)
log_qy = torch.log(qy+1e-20)
g = torch.log(torch.Tensor([1.0/x.shape[1]]))
KLD = torch.sum(qy * (log_qy - g), dim=-1).mean()
return BCE + KLD
def run(temp, epochs, n_objects, training_data_batches, n_signals, anneal_rate, temp_min, learning_rate=1e-3):
model = VAE_gumbel(temp, n_objects, n_signals)
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
for epoch in range(epochs):
total_loss = 0
for batch_idx, data in enumerate(training_data_batches):
optimizer.zero_grad()
recon_batch, qy = model(data, temp)
loss = loss_function(recon_batch, data, qy)
loss.backward()
optimizer.step()
total_loss += loss
# every 100 steps, diminish the temperature up until it's temp_min
if batch_idx % 100 == 0:
temp = np.maximum(temp*np.exp(-anneal_rate*batch_idx), temp_min)
print(total_loss)
print(temp)
return model
I have ran it e.g. with the following parameters:
n_objects, n_signals = 10, 10
n_batches, size_batch, epochs = 500, 20, 20
temp = 1.
temp_min = 0.1
anneal_rate = 1e-4
learning_rate = 1e-2
But I tested various parameter combinations and it does not seem to make much of a difference. E.g. when running the following:
input_onehots = torch.eye(n_signals)
probs_signals = trained_model.language
plt.pcolormesh(probs_signals)
plt.xlabel("signal")
plt.ylabel("state")
plt.colorbar()
plt.show()
I get this type of language:
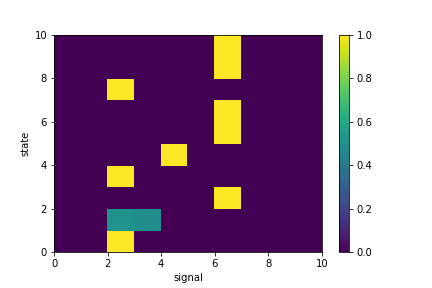
Clearly, my network is getting stuck despite the task having a simple solution. So, my question is: what is causing this problem? And related to this: how do I improve performance? is this type of problem discussed in some paper? Thank you for the help!