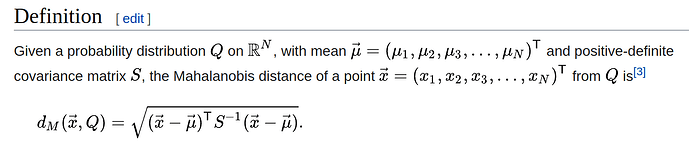What kind of approach is this to taking the Mahalanobis Distance?
I’m looking in the source code of PyTorch in distributions and the Mahalanobis Distance does not look anything like the typical equation you see returned when looking up the equation online.
Can I have some insight into what is happening here?
def _batch_mahalanobis(bL, bx):
n = bx.size(-1)
bx_batch_shape = bx.shape[:-1]
# Assume that bL.shape = (i, 1, n, n), bx.shape = (..., i, j, n),
# we are going to make bx have shape (..., 1, j, i, 1, n) to apply batched tri.solve
bx_batch_dims = len(bx_batch_shape)
bL_batch_dims = bL.dim() - 2
outer_batch_dims = bx_batch_dims - bL_batch_dims
old_batch_dims = outer_batch_dims + bL_batch_dims
new_batch_dims = outer_batch_dims + 2 * bL_batch_dims
# Reshape bx with the shape (..., 1, i, j, 1, n)
bx_new_shape = bx.shape[:outer_batch_dims]
for (sL, sx) in zip(bL.shape[:-2], bx.shape[outer_batch_dims:-1]):
bx_new_shape += (sx // sL, sL)
bx_new_shape += (n,)
bx = bx.reshape(bx_new_shape)
# Permute bx to make it have shape (..., 1, j, i, 1, n)
permute_dims = (list(range(outer_batch_dims)) +
list(range(outer_batch_dims, new_batch_dims, 2)) +
list(range(outer_batch_dims + 1, new_batch_dims, 2)) +
[new_batch_dims])
bx = bx.permute(permute_dims)
flat_L = bL.reshape(-1, n, n) # shape = b x n x n
flat_x = bx.reshape(-1, flat_L.size(0), n) # shape = c x b x n
flat_x_swap = flat_x.permute(1, 2, 0) # shape = b x n x c
M_swap = torch.linalg.solve_triangular(flat_L, flat_x_swap, upper=False).pow(2).sum(-2) # shape = b x c
M = M_swap.t() # shape = c x b
permuted_M = M.reshape(bx.shape[:-1]) # shape = (..., 1, j, i, 1)
permute_inv_dims = list(range(outer_batch_dims))
for i in range(bL_batch_dims):
permute_inv_dims += [outer_batch_dims + i, old_batch_dims + i]
reshaped_M = permuted_M.permute(permute_inv_dims) # shape = (..., 1, i, j, 1)
return reshaped_M.reshape(bx_batch_shape)