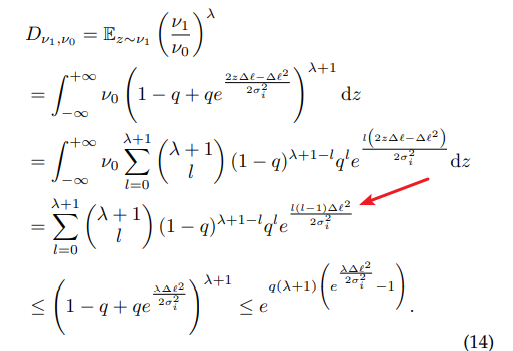privacy_engine = PrivacyEngine(centralized_model,
batch_size=256,
sample_size=50000,
alphas=range(2,32),
noise_multiplier=1.3,
max_grad_norm=1.0,)
privacy_engine.attach(centralized_optimizer)
The current noise increase parameter is bound to the optimizer, which means that each gradient descent can only use the same coefficient, and if I want to automatically change the noise coefficient, how can I make the gradient descent, and how to get the current privacy budget
Hi @jeff20210616,
Thank you for using Opacus!
I believe the question is, how can you dynamically change the noise parameter and how to get the current privacy budget accordingly. If so, Opacus certainly supports that!
New Opacus (any version > 1.0) supports dynamic privacy parameters. This is handled by scheduler: (See “Dynamic Privacy Parameters” in https://github.com/pytorch/opacus/releases/tag/v1.0.0)
I also realized that you are using the old Opacus (e.g. you have the method privacy_engine.attach()). To take advantage of dynamic privacy and other useful features of Opacus, please use the newest Opacus version  https://github.com/pytorch/opacus/blob/main/Migration_Guide.md
https://github.com/pytorch/opacus/blob/main/Migration_Guide.md
I have a other question, I read the pepar and the code, I find the default cropping norm is 1 where sensitivity is 1 , and if I crop norm is not 1 ,how can I call use privacy analysis interface?
Hi,
You can use any clipping value and noise value that you would like. Once you define your noise value and clipping value, you can call
eps = privacy_engine.get_epsilon(delta=target_delta)
to get the privacy budget.
I mean in your code library , I find some problem there
In the analysis, it is assumed that the gradient has normed bounded by 1 and the noise is of std sigma (per coordinate). The key thing is that if we multiply the gradient bound by C, we also multiply the noise by C: the noise we add has in effect a standard deviation of sigma * C.
See opacus/optimizers/optimizer.py:
in fact , my question is not about the STD. I know the sigma include the sensitivity . I think what you consider is the distribution of neighboring datasets with sensitivity 1 :
You can compare the theorem below
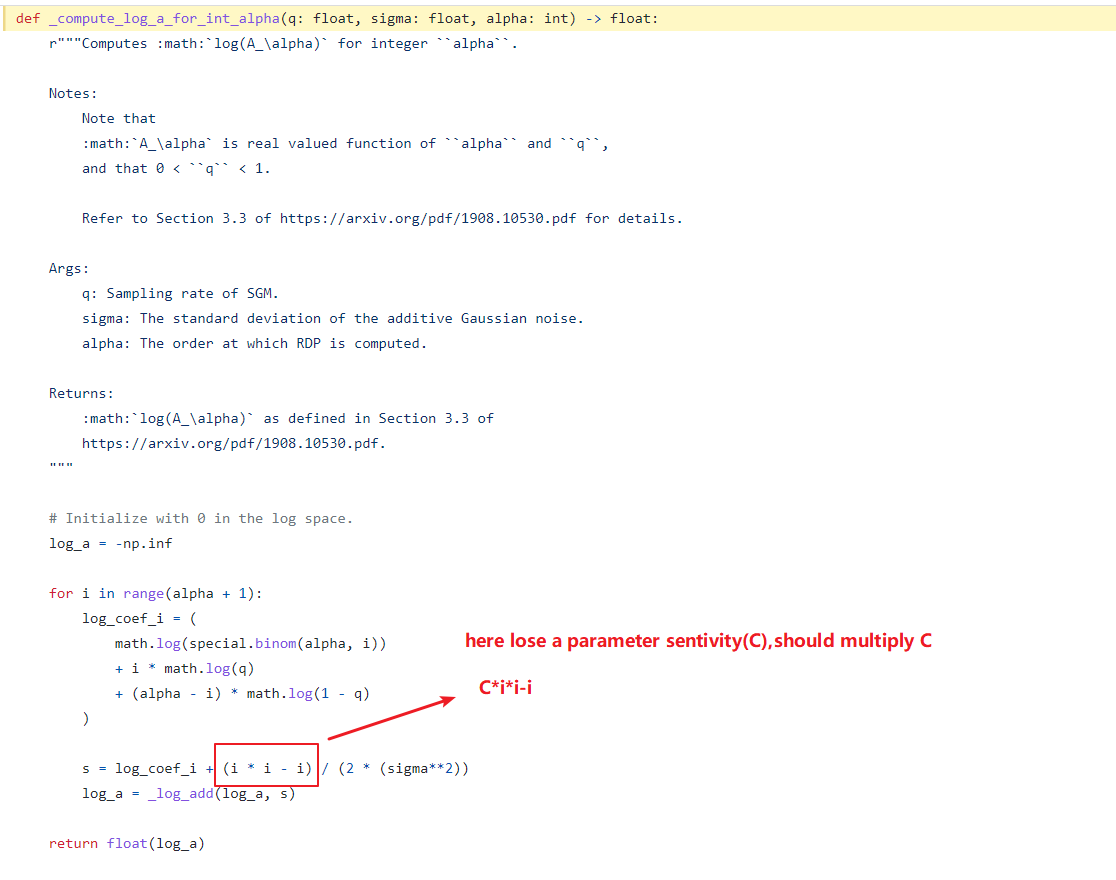
you can see that. if this function have the sensitivity is u. there is a parameter u in the proposition. it’is not about the sigma. and if the sensitivity is 1. we can write : a/2*sigma**2.but if is not 1,just like this:
and I think there is only one explanation, that the sigma in your code doesn t contain the sensitivity and the sensitivity has been offset.That is, the calculation of the RDP is independent of the sensitivity
and I noticed that here may be loss the coefficient : 1/(aplha-1)
Exactly. Both the gradient and the noise are multiplied by C. So if you look at (gradient / C), then this function has sensitivity 1 and thus you can deduce all the properties that you mentioned.
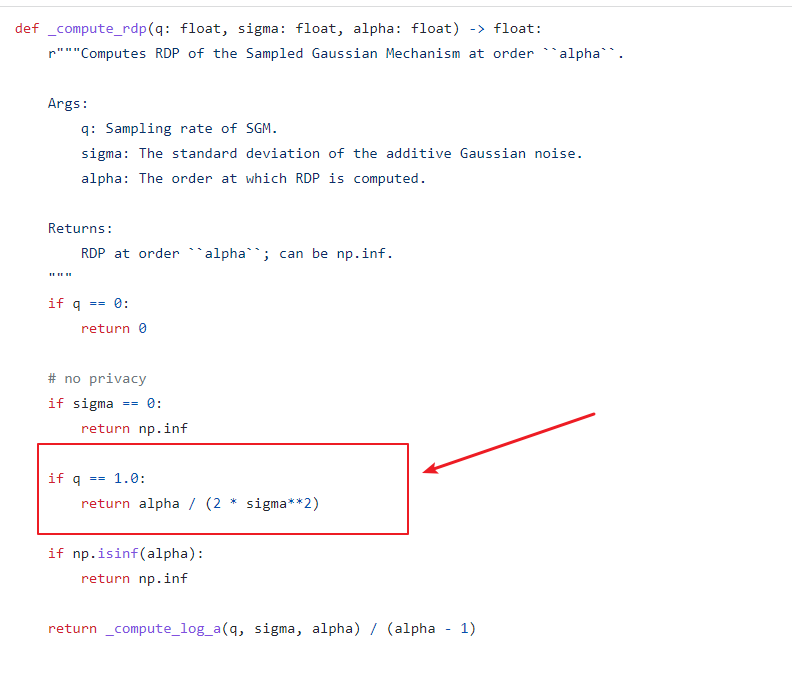
The reason here is that the two branches (q=1 and q!=1) have different ways of computing the divergence. See Section 3 of https://arxiv.org/pdf/1908.10530.pdf (where log_a is divided by alpha - 1)
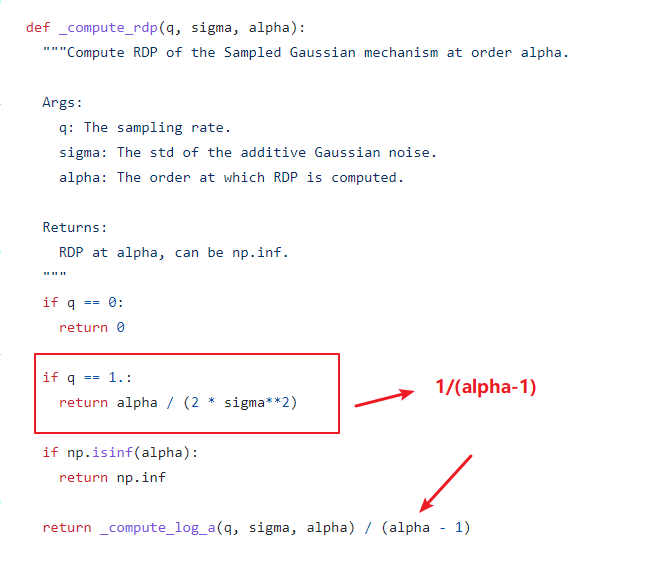
Hi @jeff20210616 , I’m not sure I follow your question. Is that not what?
yes,thank you. I mean whatever q=1 or q!=1, the equation of RDP has this coefficient:1/(alpha-1).Maybe I have some problems with my understanding.
I’m sensing the confusion is due to the notations.
Ofcourse, the 1/(alpha-1) term does appear in the Rényi Divergence formula. However, when q=1 (i.e., when sampling ratio is 1), there is essentially no sampling. The RDP of a Gaussian Mechanism is derived to be equal to alpha/(2 * sigma^2) as written in the code (see proposition 7 of https://arxiv.org/pdf/1702.07476.pdf)
1 Like
OK, I get it . thank you very much
I get it . thank you very much.
I have last question: Is the data sampled here with any put back(replace=true) or no put back(replace=flase)?