How to customize/define a loss function like this?

autograd
1

I have a network and the input has the shape like: batch x 6 x 180 x 320 ( 6channels ), after several layers of convolutions and convolution transpose, the output is of the shape: batch x 2 x180 x 320(2channels).
Suppose the element of the first channel is U, and the second channel is V,
and I want to define a loss like:
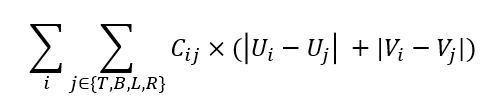
image
i is the i th element of the second channel of the output, j denotes his 4 surrounding neighbor elements(left bot, up, right)
Cij is a weight calculated from the input.
So is there a sufficient way to calculate this loss, I’ve read autograd
But according to my loss definition, I think I have to iterate the elements of two channels but is it possible?
Thanks!

2

For efficiency, you’ll want to use tensor operations instead of looping over every element.

Something like:

output = ... # batch x 2 x 180 x 320
u = output[:, 0, :, :]
v = output[:, 1, :, :]

def delta_neighbors(x):
  assert x.dim() == 3
  x = x.unsqueeze(1)  # view as 4D: batch x 1 x h x w
  padded = F.pad(x, (1, 1, 1, 1))  # pad with zeros on each side
  padded = padded.squeeze(1)  # view as 3D
  top = padded[:, :-2, 1:-1]
  bottom = padded[:, 2:, 1:-1]
  left = padded[:, 1:-1, :-2]
  right = padded[:, 1:-1, 2:]
  return (padded - top).abs() * c[0] + (padded - bottom).abs() * c[1] + (padded - left).abs() * c[2] + (padded - right).abs() * c[3]

loss = delta_neighbors(u).sum() + delta_neighbors(v).sum()
3

Thanks! I will try it.

4

I find the size of x is equal to top , bot ,left ,right not padded
so

output = … # batch x 2 x 180 x 320
u = output[:, 0, :, :]
v = output[:, 1, :, :]

def delta_neighbors(x):
assert x.dim() == 3
x = x.unsqueeze(1) # view as 4D: batch x 1 x h x w
padded = F.pad(x, (1, 1, 1, 1)) # pad with zeros on each side
padded = padded.squeeze(1) # view as 3D
top = padded[:, :-2, 1:-1]
bottom = padded[:, 2:, 1:-1]
left = padded[:, 1:-1, :-2]
right = padded[:, 1:-1, 2:]
return (x - top).abs() * c[0] + (x - bottom).abs() * c[1] + (x - left).abs() * c[2] + (x - right).abs() * c[3]

loss = delta_neighbors(u).sum() + delta_neighbors(v).sum()