Hi,
Given an input tensor (1x3xNxN) representing an image which undergoes many 2d convolutions/maxpool transformations, I obtain an output tensor (1xKxMxM) with K an arbitrary number of dimension (one per filter of the last layer) and M the side of the output tensor.
What I would like to do, is given a slice Z in the output generated by one of the K final filters
Z=([x1,x2],[y1,y2]) with 0 <= x1 <= x2 <= M, 0 <= y1<= y2 <= M,
recover the original input slice Z’=([x1’,x2’],[y1’,y2’]) with
0<= x1’ <= x2’ <= N ,0<= y1’<=y2’<=N
which was the crop of the image which allowed to generate the area in the output layer. I already have a working code for a single convolutional layer and a “single-pixel” (x1’=x2’=x) output interval:
x1’ = max(x S-P,0) x2’ = min(xS +K-P,N)
where S = stride size, P = padding, K = kernel size, N = input size
Is there a way to obtain this using pytorch code exclusively? The current approach would be far from ideal. Thank you for any help!
I’m not sure I understand the question completely, so please correct me if I’m wrong.
Based on the formulas it seems you would like to calculate the receptive field on the convolutions given a specific output activation?
Excuse me for the clumsy explanation: my goal is to calculate the receptive field in the original layer for a given field in the output one.
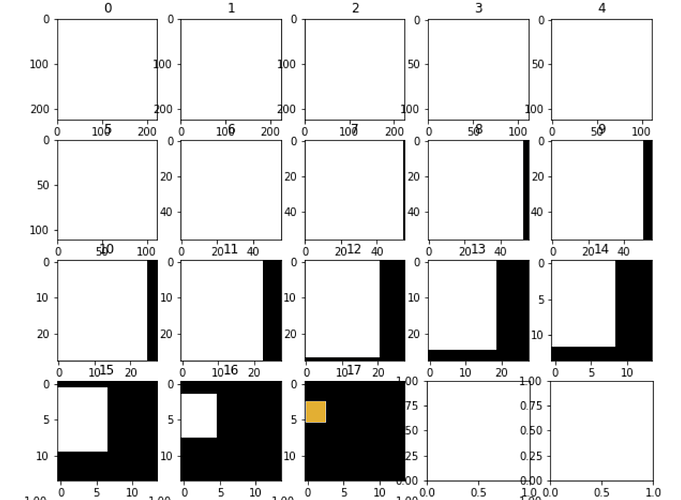
The figure represents an image (3x224 x 224) going through 17 Conv2d and Maxpool layers (one layer between each frame of the figure,please ignore the last 2 frames) I plot in orange the slice of interest in the output tensor: what I am looking for is a way to recover the white slices for each intermediate frame,i.e the portion of the previous tensor which will generate the next on,everything based on the slice of interest of the last tensor (orange)
You could calculate the receptive field manually using the conv and pooling setup, but that is of course quite tedious.
I’m not sure, if there are any libraries providing this functionality with this kind of visualization.
However, I found this repo which uses a gradient based approach and could thus be suitable for more complex models.
Thank you very much! It looks like it should do!