Can someone give an idea on how to implement k-means clustering loss in pytorch?
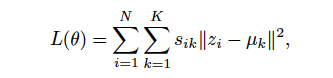
Also I am using Pytorch nn.mse() loss. Is there a way to add L2 reguarization to this term. In short, if I want to use L2-Reg. loss.
Can someone give an idea on how to implement k-means clustering loss in pytorch?
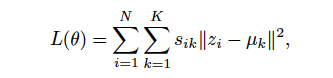
Also I am using Pytorch nn.mse() loss. Is there a way to add L2 reguarization to this term. In short, if I want to use L2-Reg. loss.
Could you explain, what s_ik is?
Which parameter do you want to use the L2 reg. on?
@ptrblck
For the K-means loss, this is what I am doing. I just want to verify if its correct . Or is there any other clean way of doing this?
import torch
class KMeansClusteringLoss(torch.nn.Module):
def __init__(self):
super(KMeansClusteringLoss,self).__init__()
def forward(self, encode_output, centroids):
assert (encode_output.shape[1] == centroids.shape[1]),"Dimensions Mismatch"
n = encode_output.shape[0]
d = encode_output.shape[1]
k = centroids.shape[0]
z = encode_output.reshape(n,1,d)
z = z.repeat(1,k,1)
mu = centroids.reshape(1,k,d)
mu = mu.repeat(n,1,1)
dist = (z-mu).norm(2,dim=2).reshape((n,k))
loss = dist.min(dim=1)[0].mean()
return losss_ik is bascially one-hot vector which is 1 if data point i belongs to cluster k.
And for L2-reg. I simply want to implement Ridge Regression: Loss + \lambda || w ||_2.
where \lambda would be a hyperparameter and Loss = nn.mse().
I’d probably not use repeat but let the broadcasting do it’s thing. Also, personally I prefer unsqueeze or indexing (z = z[None, :, :]) over reshape to get the new dimensions.
Best regards
Thomas
@tom Can you please explain a bit on how exactly should this be done? And is there some advantage of using broadcasting over repeat ?
If you use triple backticks (```python) before and just the backtics (```) after your code, it will be well-formatted.
In Jupyter:
import torch
class KMeansClusteringLoss(torch.nn.Module):
def __init__(self):
super(KMeansClusteringLoss,self).__init__()
def forward(self, encode_output, centroids):
assert (encode_output.shape[1] == centroids.shape[1]),"Dimensions Mismatch"
n = encode_output.shape[0]
d = encode_output.shape[1]
k = centroids.shape[0]
z = encode_output.reshape(n,1,d)
z = z.repeat(1,k,1)
mu = centroids.reshape(1,k,d)
mu = mu.repeat(n,1,1)
dist = (z-mu).norm(2,dim=2).reshape((n,k))
loss = (dist.min(dim=1)[0]**2).mean() # note that you didn't have the square loss as the equation
return loss
def sq_loss_clusters(encode_output, centroids):
assert encode_output.size(1) == centroids.size(1), "Dimension mismatch"
return ((encode_output[:, None]-centroids[None])**2).sum(2).min(1)[0].mean()
loss_fn = KMeansClusteringLoss()
pts = torch.randn(2000,10)
means = torch.randn(10,10)
l1 = loss_fn(pts, means)
l2 = sq_loss_clusters(pts, means)
assert (l1==l2).all()
%timeit loss_fn(pts, means)
%timeit sq_loss_clusters(pts, means)
has 3.07ms for your version and 684µs for mine, so it’s >4 faster.
I think it’s more clear what’s going on, too, if you write it more concise (maybe add a comment linking to the equation and commenting that s_ik == 1 if the assignment of point i to cluster k is optimal given fixed centers, or spread it over several lines to be better able to follow - tastes vary and that is fine).
Note that the equation you posted had the square distance, so I used that.
Best regards
Thomas
@tom Thank you so much. I will try this out.
Could you also guide on how to use L2-regularization with Mean Squared Error loss?
Well, either use the weight decay of the optimizers (which adds a multiple the derivative of |w|² to the gradient) or sum |w|² yourself (reg_loss = sum([p**2 for p in m.parameters()] or so should work).
Best regards
Thomas
I’m not an expert on this, my rule of thumb would be to use built-in weight decay for efficiency if it works for you.
But really, I don’t have any profound insights to offer here.
Best regards
Thomas