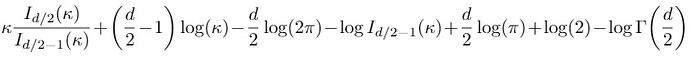Modified Bessel Function of Order 0

autograd
1

How to implement modified bessel functions in Pytorch? Any ideas/hints?

2

For a CPU only version, you could use scipy.special

import scipy.special
# note, we do not differentiate w.r.t. nu
class ModifiedBesselFn(torch.autograd.Function):
    @staticmethod
    def forward(ctx, inp, nu):
        ctx._nu = nu
        ctx.save_for_backward(inp)
        return torch.from_numpy(scipy.special.iv(nu, inp.detach().numpy()))
    @staticmethod
    def backward(ctx, grad_out):
        inp, = ctx.saved_tensors
        nu = ctx._nu
        # formula is from Wikipedia
        return 0.5* grad_out *(ModifiedBesselFn.apply(inp, nu - 1.0)+ModifiedBesselFn.apply(inp, nu + 1.0)), None
modified_bessel = ModifiedBesselFn.apply

Then you can check that it works:

x = torch.randn(5, requires_grad=True, dtype=torch.float64)
torch.autograd.gradcheck(lambda x: modified_bessel(x, 0.0), (x,))

If you wanted to do this for cuda, too, you would have to write your own kernel (or open an issue at the PyTorch github).

The differentiation w.r.t. $nu$ seems more tricky, I don’t know whether it has a closed from solution.

Best regards

Thomas

1 Like
3

Thanks Tom,

This might be very naiive. But, I hope it is possible to just compute the backward pass for the variables related to Bessel in CPU and rest in GPU?

4

Hi @tom, what do you mean by

write your own kernel

I need to compute the KL divergence of two von Mises-Fisher distributions for a variational loss function. Right now I do the computation with scipy. My GPU utility is very low (most of the time close to zero percent usage), I guessed that the reason is that the computation of the scipy is carried out on the CPU and then transferred to GPU. Therefore I would like to do all the computation on the GPU.

5

You’d need to write a fuction for that yourself, but depending on what operations you need, you might be able to use the fuser, or write a cuda kernel. What is the formula for your calculation?

Best regards

Thomas

6

Thank you @tom I have finally computed the KL term separately with scipy and then moved it to GPU, the gradient is not with respect to kappa so I think there shouldn’t be any problem. This is the KL-divergence term I would like to compute:

kld
kld831×69 14.9 KB

d is the dimesntion of the latent space.

7

How do you succeeded in using Bessel function without Scipy? I have a similar problem now.

8

have u finished pytorch GPU version of Modified Bessel functions?