Hi,
I am trying to execute a version of multi headed attention on input batches of sequence length 10. Below is a simplified version of my code:
type or paste code here
class MultiHeadAttention(nn.Module):
# Multi-Head Attention module
def __init__(self, n_head, d_model, embed_dim_per_head, dropout=0.1):
super().__init__()
total_embed_dim = embed_dim_per_head * n_head
self.w_qs = nn.Linear(d_model, total_embed_dim, bias=False)
self.w_ks = nn.Linear(d_model, total_embed_dim, bias=False)
self.w_vs = nn.Linear(d_model, total_embed_dim, bias=False)
self.fc = nn.Linear(total_embed_dim, d_model)
self.attention = nn.MultiheadAttention(
embed_dim = total_embed_dim,
num_heads = n_head,
dropout = 0.1)
self.dropout = nn.Dropout(dropout)
self.layer_norm = nn.LayerNorm(d_model, eps=1e-6)
def forward(self, q, k, v):
residual = q
# NB, SEQ_LEN, (N_HEAD * D) -> SEQ_LEN, NB, (N_HEAD * D)
q = self.w_qs(q).permute(1, 0, 2)
k = self.w_ks(k).permute(1, 0 ,2)
v = self.w_vs(v).permute(1, 0, 2)
q, att_map = self.attention(q, k, v, need_weights=True)
print(f'AttMap Max Values: {att_map[0].max(dim=-1)[0]}')
# SEQ_LEN, NB, (N_HEAD * D) -> NB, SEQ_LEN, (N_HEAD * D)
q = q.permute(1, 0, 2)
q = self.dropout(self.fc(q))
q += residual
q = self.layer_norm(q)
return q
class IntraModal_MHA(nn.Module):
def __init__(self, num_blocks, num_heads, transform_dim, embed_dim_per_head, activation):
super(IntraModal_MHA, self).__init__()
self.activation = activation
self.num_blocks = num_blocks
self.mha_list = nn.ModuleList([
MultiHeadAttention(num_heads, transform_dim, embed_dim_per_head)
for i in range(num_blocks)])
self.linear_list = nn.ModuleList([
nn.Sequential(
nn.Linear(transform_dim, 2 * transform_dim),
self.activation,
nn.Dropout(0.1),
nn.Linear(2 * transform_dim, transform_dim),
self.activation,
nn.Dropout(0.1),
)
for i in range(num_blocks)])
self.layer_norms = nn.ModuleList([
nn.LayerNorm(transform_dim, eps=1e-6)
for i in range(num_blocks)])
def forward(self, modal_ft):
for i in range(self.num_blocks):
output = self.mha_list[i](modal_ft, modal_ft, modal_ft)
residual = output
output = self.linear_list[i](output)
output += residual
modal_ft = self.layer_norms[i](output)
return modal_ft
class A2H(nn.Module):
def __init__(self):
super(A2H, self).__init__()
self.activation = nn.ReLU(inplace=True)
self.audio_transform = nn.Sequential(
nn.Linear(128, 512),
self.activation,
nn.Dropout(0.1),
)
self.a2a_temporal_att = IntraModal_MHA(1, 1, 512, 512, self.activation)
self.classifier_fc = nn.Linear(512, 29)
@staticmethod
def positional_encoding(n_position, emb_dim):
#The sinusoid position encoding table
position_enc = np.array([
[pos / np.power(10000, 2 * (j // 2) / emb_dim) for j in range(emb_dim)]
for pos in range(n_position)])
position_enc[:, 0::2] = np.sin(position_enc[:, 0::2]) # dim 2i
position_enc[:, 1::2] = np.cos(position_enc[:, 1::2]) # dim 2i+1
return torch.from_numpy(position_enc).type(torch.FloatTensor)
def forward(self, audio_ft, unused_):
nb, seq_len, aud_ft_dim = audio_ft.shape
audio_ft_pe = audio_ft + self.positional_encoding(seq_len, aud_ft_dim).cuda()
audio_ft_pe = self.audio_transform(audio_ft_pe)
a2a_temporal_out = self.a2a_temporal_att(audio_ft_pe)
signal_out = self.classifier_fc(a2a_temporal_out)
classifier_out = F.softmax(signal_out, dim=-1)
return classifier_out
My optimizer is the typical SGD with momentum setting with a high LR of 0.2.
Below are the outputs for my prints which display
- The gradients to the nn.Linear which transforms my input into Query and Key matrices
- The maximum value of the 1st batch’s attention returned by nn.MultiheadAttention:
After Update:
a2a_temporal_att.mha_list.0.w_qs.weight : 3.750015922787675e-12
a2a_temporal_att.mha_list.0.w_ks.weight : 3.718521150719578e-12
AttMap Max Values: tensor([0.1128, 0.1126, 0.1123, 0.1128, 0.1134, 0.1130, 0.1128, 0.1122, 0.1121,
0.1125], device=‘cuda:0’, grad_fn=)
After Update:
a2a_temporal_att.mha_list.0.w_qs.weight : 4.729227426336635e-12
a2a_temporal_att.mha_list.0.w_ks.weight : 4.986864220180021e-12
AttMap Max Values: tensor([0.1131, 0.1140, 0.1128, 0.1137, 0.1142, 0.1136, 0.1132, 0.1129, 0.1123,
0.1122], device=‘cuda:0’, grad_fn=)
After Update:
a2a_temporal_att.mha_list.0.w_qs.weight : 2.1090891186292815e-11
a2a_temporal_att.mha_list.0.w_ks.weight : 1.926272509555904e-11
AttMap Max Values: tensor([0.1123, 0.1121, 0.1126, 0.1123, 0.1123, 0.1122, 0.1118, 0.1124, 0.1122,
0.1123], device=‘cuda:0’, grad_fn=)
After Update:
a2a_temporal_att.mha_list.0.w_qs.weight : 1.62918636914533e-11
a2a_temporal_att.mha_list.0.w_ks.weight : 1.50868172121843e-11
As you can see my implementation of IntraModal_MHA contains residual connections to avoid the vanishing gradient problem and resembles to that of the transformer structure.
Below is the gradient accumulation for the entire network in the 6th epoch during which my accuracy increased from 28% to 33%:
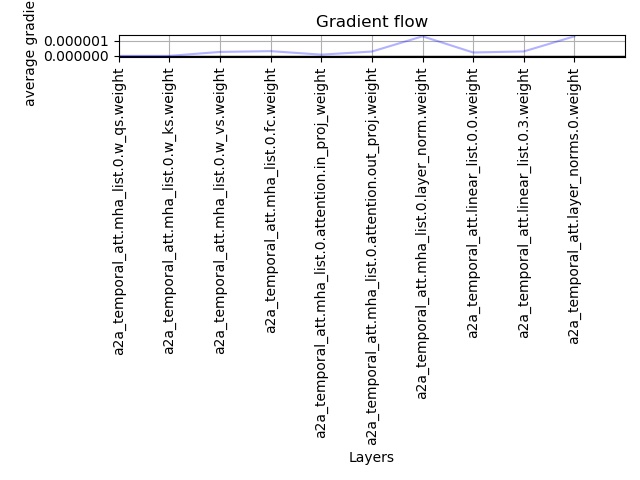
The gradients to both the w_qs and w_ks are always super low and the attention map is not converging into a sharp distribution. The input sequences contain foreground and background type samples and the objective is to classify the foreground samples. From the above objective, the attention map is expected to be sharp. Additionally, as I increase the complexity of the network by increasing the number of blocks in the IntraModal_MHA, the gradients become even more smaller.
Has anyone faced this or can someone please point out any obvious mistake I might be doing?
Thanks a lot!