Multiple losses, ignored when multiplied by scalar

autograd
1

Hi,
I try to implement a stabilized attack method, which consist of a classical iterative fast gradient sign method (FGSM) plus a stabilization term.

Here is the definition of the loss stabilized (W is gaussian kernel, eta the sign grad through iteration) :
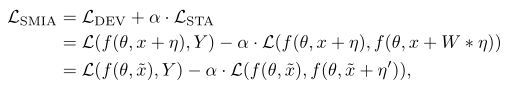
smia_attack

Below my implementation

def smia_attack(image, epsilon, alpha, model, target, n_step):

    attack_image = image.detach().requires_grad_()

    L_dev = F.nll_loss(model(attack_image), target)
    model.zero_grad()
    L_dev.backward()
    grad_image = attack_image.grad.data
    sign_grad_image = grad_image.sign()
    
    eta = epsilon*sign_grad_image
    W = gaussianBlur(10, 3, 1).cuda()
    for i in range(n_step):
        with torch.no_grad():
            attack_image.add_(eta)
            attack_image = attack_image.clamp(0, 1).detach().requires_grad_()
        model.zero_grad()
        L_smia = F.nll_loss(model(attack_image), target) - alpha * F.nll_loss(model(attack_image), model(attack_image + W(eta) - eta).argmax().unsqueeze(0))
        L_smia.backward()
        eta = epsilon * attack_image.grad.data.sign()
    return attack_image + eta

When I generate perturbed images, Pytorch seems to ignore the right parrt of L_smia, namely : -alpha *F.nll_loss (…) because if I remove it, nothing changes, and I have the exact same result without, ie, it’s doing vanilla FGSM.
However, if I remove the alpha term, then the result is pretty different, Pytorch seems to make us of it.

Any idea why ?

2

Hi,

Note that it would be better to replace:

        L_smia.backward()
        eta = epsilon * attack_image.grad.data.sign()

by

        grad, = autograd.grad(L_smia, attack_image)
        eta = epsilon * grad

For your issue, what is the value of alpha?
Also you can check the gradients flowing back by using hooks: on any Tensor, you can set t.register_hook(your_fn). So that your_fn will be called for the gradient for that Tensor. That way you can check what are the gradient values flowing on the right part of your model.