Operations on subset of tensor, which to use?

1

I often need to conduct scalar operation (e.g. add or multiply) on a subset of tensor elements, where the subset is specified by another tensor in a form of index or mask.
There are multiple ways of doing this, and I would like to know which to use or which is better.
I myself conducted a few experiments of speed comparison (details below).
In short, the result was that indexing (using long or byte) tends to be slower than updating the whole tensor.

Question

I would like to know pros and cons of different ways to update a subset of tensor. In particular, should we avoid subset updating in a form x[cond] = ... if other options are available?

Below describes the experiments that I made.

Operation on subset of rows

Let X be a float tensor on which changes are made, and a is a scalar. Suppose we want to add a to as subset rows of X.
As far as I know, there are following ways of doing this:

  • X[idx] += a, where idx is a long 1-D tensor of indices.
  • X[mask] += a, where mask is a byte 1-D tensor of conditions.
  • X += mask_f * a, where mask_f is a float 1-D tensor of conditions.

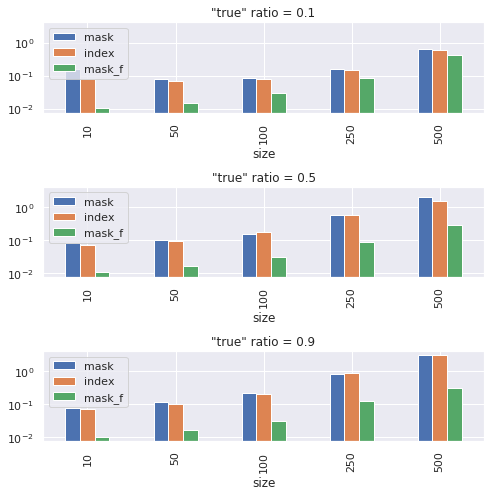
Graph below is the time for 1000 operations. “true” ratio is the fraction of rows satisfying the condition. Size is the size of rows and columns of X.
X += mask_f * a tends to be faster for many cases, but “indexing” may outperform with small p (only few rows satisfy condition) and large tensor size.
download%20(2)

Operation on subset of elements

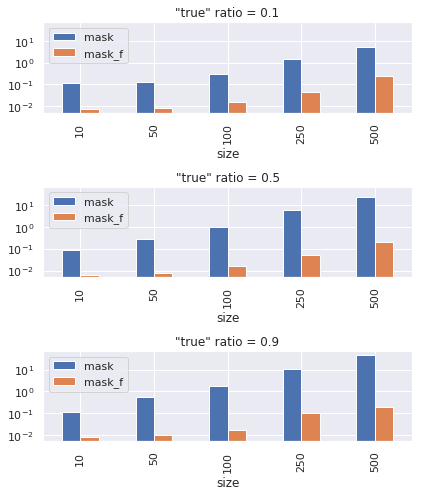
Now suppose we have a element-wise condition in a form of mask. And we would like to add a only to the elements of X where condition is satisfied. I know the following two ways.

  • X[mask] += a, where mask is a byte tensor of conditions with same size as X.
  • X += mask_f * a, where mask_f is a float tensor of conditions with same size as X.

Again, X += mask_f * a is faster.
download%20(1)

Code to reproduce (up to randomness).

import timeit
import random
import torch
import numpy as np
number = 1000
y = 4.0
setup = """from __main__ import x, y, mask, idx, mask_f"""
out = []

for p in [0.1, 0.5, 0.9]:
    for s in [10, 50, 100, 250, 500]:
        x0 = np.random.random((s, s))
        mask = np.array(random.choices([True, False], weights=[p, 1-p], k=s), dtype=np.uint8)
        idx = np.where(mask)[0]
        mask = torch.tensor(mask, dtype=torch.uint8)
        idx = torch.tensor(idx, dtype=torch.long)
        mask_f = mask.float().view(-1, 1)

        x = torch.tensor(x0, dtype=torch.float32)
        t1 = timeit.timeit("x[mask] += y", setup=setup, number=number)    
        x1 = x.numpy()

        x = torch.tensor(x0, dtype=torch.float32)
        t2 = timeit.timeit("x[idx] += y", setup=setup, number=number)
        x2 = x.numpy()

        x = torch.tensor(x0, dtype=torch.float32)
        t3 = timeit.timeit("x += mask_f * y", setup=setup, number=number)
        x3 = x.numpy()
        assert np.all(x1 == x2)
        assert np.all(x1 == x3)
        out.append([s, p, t1, t2, t3])

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

df = pd.DataFrame(out, columns=["size", "true_ratio", 
                                "mask", "index", "mask_f"]).set_index(["true_ratio", "size"])
fig, axes = plt.subplots(3, 1, figsize=(7, 7), sharey=True)
for i, p in enumerate(df.index.levels[0]):
    ax = axes[i]
    df.loc[p].plot(kind="bar", ax=ax)
    ax.set_yscale("log")
    ax.set_title('"true" ratio = ' + str(p))
fig.tight_layout()


y = 4.0
number = 1000
setup = """from __main__ import x, y, mask, mask_f"""
out = []
for p in [0.1, 0.5, 0.9]:
    for s in [10, 50, 100, 250, 500]:
        x0 = np.random.random((s, s))
        mask = np.array(random.choices([True, False], weights=[p, 1-p], k=s*s), dtype=np.uint8).reshape((s, s))
        mask = torch.tensor(mask, dtype=torch.uint8)
        mask_f = mask.float()

        x = torch.tensor(x0, dtype=torch.float32)
        t1 = timeit.timeit("x[mask] += y", setup=setup, number=number)    
        x1 = x.numpy()

        x = torch.tensor(x0, dtype=torch.float32)
        t2 = timeit.timeit("x += mask_f * y", setup=setup, number=number)
        x2 = x.numpy()
        
        assert np.all(x1 == x2)
        out.append([s, p, t1, t2])

df = pd.DataFrame(out, columns=["size", "true_ratio", "mask", "mask_f"]).set_index(["true_ratio", "size"])
fig, axes = plt.subplots(3, 1, figsize=(6, 7), sharey=True)

for i, p in enumerate(df.index.levels[0]):
    ax = axes[i]
    df.loc[p].plot(kind="bar", ax=ax)
    ax.set_yscale("log")
    ax.set_title('"true" ratio = ' + str(p))
fig.tight_layout()
1 Like