Hi everyone,
I had some thoughts on the gaussian prior on VAE latent variables. For instance, Kingma et al. in the original paper ([1312.6114] Auto-Encoding Variational Bayes) illustrated the manifold learned on MNIST data by a VAE with 2 latent variables.
Let’s say for the sake of the argument that images whose latent variables are around (0,0) are images of 3. The gaussian prior being centered at zero, 3 images will be more likely to be generated than sixes or tens…
If I understand it right, this is clearly an unwanted side effect of the gaussian priors.
Does anyone have an opinion on this ?
Thanks,
Happy Christmas all,
Matheo
I think you wouldn’t normally sample from prior, beyond some diagnostic plots (even then, note that paper you linked uses quantiles for that plot). So, yeah, posterior clusters are scattered around zero randomly, but encoder deals with that.
Hi @googlebot thanks for the reply although it seems (from some papers and from this topic: machine learning - When generating samples using variational autoencoder, we decode samples from $N(0,1)$ instead of $\mu + \sigma N(0,1)$ - Cross Validated) that sampling from the prior is the usual way.
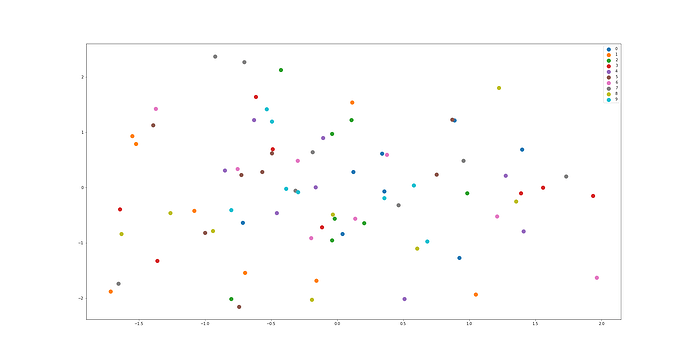
I have another interrogation that is related to the first one: I have trained a conditional 2-latent variables VAE on MNIST dataset. The generated images are very convincing. When plotting the latent representations of the generated samples (see figure below), I expected to see clusters which is not the case at all. This is actually what you said :
So, yeah, posterior clusters are scattered around zero randomly, but encoder deals with that.
Each color is related to a different number. X and Y axis are the two dimensional latent variables.
I’m quite puzzled, there’s obviously something I don’t get… I thought that small variations of latent variables would induce small variations in generated images as it is presented in Kingma paper on MNIST and Frey Face datasets.
What do you mean by :
note that paper you linked uses quantiles for that plot
The paper says:
since the prior of the latent space is Gaussian, linearly spaced coor-dinates on the unit square were transformed through the inverse CDF of the Gaussian to produce values of the latent variablesz. For each of these values z, we plotted the corresponding generative pθ(x|z)with the learned parameters θ
which I don’t understand.
You’d sample from prior if you don’t care which digit you generate.
Basically, clusters should overlap at zero. Your picture has too few points too infer contours. Should look like there: How well does $Q(z|X)$ match $N(0,I)$ in variational autoencoders? - Cross Validated
Re: quantiles, I just mean they didn’t use usual sampling or gaussian density, inverse CDF skews axes.
Ok thanks, it gets clearer!