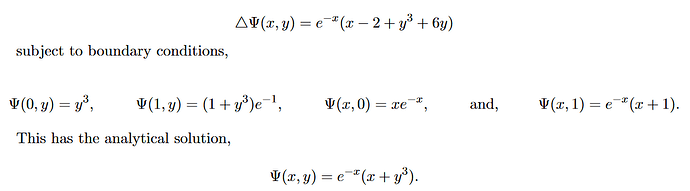Hello, I am trying to solve the following partial differential equation with 4 boundary conditions (see image)
I have written a neural network to try and solve this problem but it is not working, can anyone tell me why?
Code is below for convinence:
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
np.set_printoptions(suppress=True)
torch.set_printoptions(sci_mode=False)
torch.manual_seed(0)
HL=25
N = nn.Sequential(nn.Linear(2, HL), nn.Sigmoid(),
nn.Linear(HL, 1, bias=False))
Psi_t = lambda xy: ((1-xy[:,0])*(xy[:,1] ** 3) + xy[:,0]*(1 + (xy[:,1] ** 3))*np.exp(-1) + (1 - xy[:,1])*xy[:,0]*(torch.exp(-xy[:,0]) - np.exp(-1))
+ xy[:,1]*((1+xy[:,0])*torch.exp(-xy[:,0]) - (1 - xy[:,0] + 2*xy[:,0]*np.exp(-1))) + xy[:,0]*(1-xy[:,0])*xy[:,1]*(1-xy[:,1])*N(xy))
f = lambda xy: torch.exp(-xy[:,0])*(xy[:,0] - 2 + xy[:,1] ** 3 + 6*xy[:,1])
def data_prep(size):
x_d = ((np.linspace(0, 1, size)[:, None]).T)[0]
x_temp, y_temp = [], []
for i in range(size):
for x_i in x_d: x_temp.append(x_i)
for y_i in range(size): y_temp.append(x_temp[i])
x, y = torch.FloatTensor(x_temp).to(device), torch.FloatTensor(y_temp).to(device)
xy = torch.stack([x, y], 1)
return xy
def diff(fun, var):
return torch.autograd.grad(fun, var, grad_outputs=torch.ones_like(fun), create_graph=True)[0]
def loss(xy):
xy.requires_grad = True
outputs = Psi_t(xy)
grads, = torch.autograd.grad(outputs, xy, grad_outputs=outputs.data.new(outputs.shape).fill_(1), create_graph=True, only_inputs=True)
Psi_t_x, Psi_t_y = grads[:,0], grads[:,1]
grads_x, = torch.autograd.grad(Psi_t_x, xy, grad_outputs=Psi_t_x.data.new(Psi_t_x.shape).fill_(1), create_graph=True, only_inputs=True)
Psi_t_x_x = grads_x[:,0]
grads_y, = torch.autograd.grad(Psi_t_y, xy, grad_outputs=Psi_t_y.data.new(Psi_t_y.shape).fill_(1), create_graph=True, only_inputs=True)
Psi_t_y_y = grads_y[:,1]
lap_Psi_t = Psi_t_x_x + Psi_t_y_y
print("lap_Psi_t = \n", lap_Psi_t)
print("f(x, y) = \n", f(xy))
return torch.mean((lap_Psi_t - f(xy))**2)
optimizer = torch.optim.LBFGS(N.parameters(), lr=1e-2)
xy = data_prep(10)
def closure():
optimizer.zero_grad()
l = loss(xy)
print("loss = %.13f"% l)
l.backward()
return l
for i in range(10000):
optimizer.step(closure)
def psi(x, y):
return np.exp(-x)*(x + y**3)
x_te = np.linspace(0, 1, 100)
y_te = np.linspace(0, 1, 100)
x_test, y_test = np.meshgrid(x_te, y_te)
xy_test = data_prep(10)
Psi_t_test = Psi_t(xy_test).detach().numpy()
Psi_t_true = psi(x_test, y_test)
print("Psi_t_test = \n", Psi_t_test)
print("Psi_t_true = \n", Psi_t_true)
fig = plt.figure(dpi=1000)
ax = plt.axes(projection='3d')
ax.plot_wireframe(x_test, y_test, Psi_t_test, color='blue')
ax.plot_wireframe(x_test, y_test, Psi_t_true, color='orange')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('Psi(x, y)');