Hi I’m trying to implement a convolution that operates on a slighly different image representation.
This representation can be though of as taking an 2D image with pixel values x_i
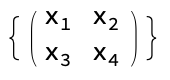
And adding some additional terms for each pixel
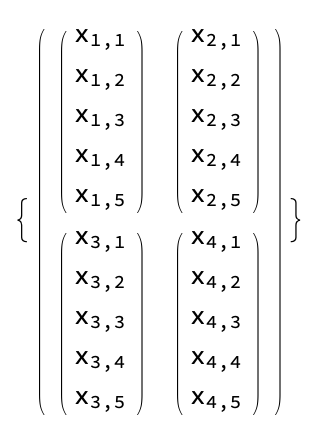
I see that this feels similar as a multi channel image, but the import difference is the inner most vectors should be treated as a single object and added element wise. For example a more complex image like
When convolved with the kernel
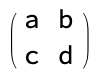
Would output this mess
The other fun twist is bias must only be added to the first element of every pixel vector.
I have a simple implementation ignoring strides and padding that looks like this
def forward(self, img):
k = self.kernel_size
# dimension of each image channel (assumes n x n)
n = img.shape[-2]
# <5> stack all output channels
return torch.stack(
# <4> take all channels, stack and sum
[torch.stack(
# <3> takes all rows and stack
[torch.stack(
# <2> take inner products across a row and stack
[torch.stack(
# <1> take inner product with kernel at top left corner pixel (l, m)
[torch.stack([kernel[i, j] * img_channel[l + i, m + j] for i in range(k) for j in
range(k)]).sum(0).index_add(0, tensor([0]), bias)
# <1>
for m in range(n - k)])
# <2>
for l in range(n - k)])
# <3>
for img_channel in img]).sum(0)
# <4>
for kernel, bias in zip(self.weight, self.bias)])
# <5>
I figured since this is really so similar to regular convolution exept that pixels are now vectors and added elementwise someone might have an idea for how I could use some pytorch builtins more effectively. Since I will be running this on a 14 core machine this nasty thing of list comprehensions will really hurt my performance.
Any ideas are much appreciated. Thanks

