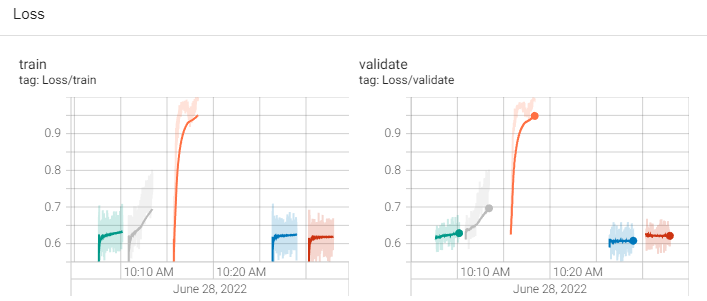
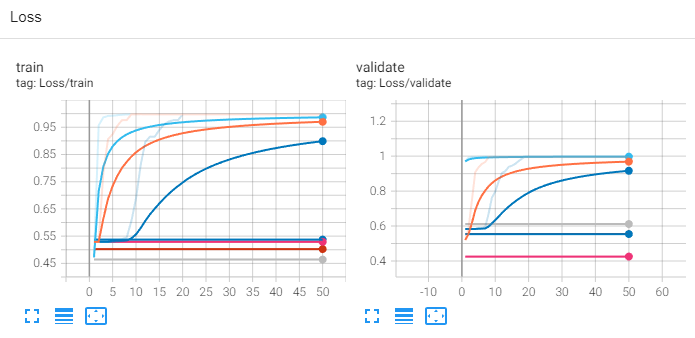
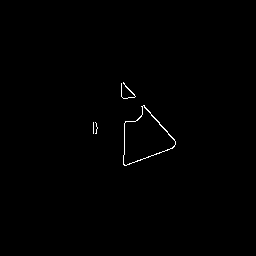Here’s the code:
Batch Generation:
import numpy as np
import random
class GenerateImageBatch:
def __init__(self, img,
lab,
batch_size):
self.img_h = img.shape[1]
self.img_w = img.shape[2]
self.img_count = img.shape[0]
self.batch_size = batch_size
self.imgs = img
self.labs = lab
self.n = img.shape[0]
self.indices = list(range(self.n))
self.cur_index = 0
self.inputs = None
self.outputs = None
''' Next sample'''
def next_sample(self):
self.cur_index += 1
if self.cur_index >= self.n:
self.cur_index = 0
random.shuffle(self.indices)
return self.imgs[self.indices[self.cur_index]], self.labs[self.indices[self.cur_index]]
''' Create next batch of images and labels to feed the NN'''
def next_batch(self):
X_data = np.zeros([self.batch_size, self.img_w, self.img_h, 1])
Y_data = np.zeros([self.batch_size, self.img_w, self.img_h, 1])
for i in range(self.batch_size):
img, lab = self.next_sample()
img = img.T
img = np.expand_dims(img, -1)
X_data[i] = img
lab = lab.T
lab = np.expand_dims(lab, -1)
Y_data[i] = lab
inputs = X_data
outputs = Y_data
self.inputs = inputs
self.outputs = outputs
Model:
import numpy as np
import torch
import torch.nn as nn
class Net(nn.Module):
def __init__(self,
batch_size,
k_gaussian=3,
k_sobel = 3,
mu=0,
sigma=3):
super(Net, self).__init__()
self.batch_size = batch_size
# Gaussian filter
gaussian_2D = self.get_gaussian_kernel(k_gaussian, mu, sigma)
self.conv1 = nn.Conv2d(in_channels=1,
out_channels=1,
kernel_size=k_gaussian,
padding=k_gaussian // 2,
padding_mode="replicate",
bias=False)
gaussian_2D = torch.from_numpy(gaussian_2D)
gaussian_2D.requires_grad = True
with torch.no_grad():
self.conv1.weight[:] = gaussian_2D
# Sobel filter x direction
sobel_2D = self.get_sobel_kernel(k_sobel)
self.conv2 = nn.Conv2d(in_channels=1,
out_channels=1,
kernel_size=k_sobel,
padding=k_sobel // 2,
padding_mode="replicate",
bias=False)
sobel_2D = torch.from_numpy(sobel_2D)
sobel_2D.requires_grad = True
with torch.no_grad():
self.conv2.weight[:] = sobel_2D
# Sobel filter y direction
self.conv3 = nn.Conv2d(in_channels=1,
out_channels=1,
kernel_size=k_sobel,
padding=k_sobel // 2,
padding_mode="replicate",
bias=False)
with torch.no_grad():
self.conv3.weight[:] = sobel_2D.T
# Hysteresis custom kernel
self.conv4 = nn.Conv2d(in_channels=1,
out_channels=1,
kernel_size=3,
padding=1,
padding_mode="replicate",
bias=False).cuda()
hyst_kernel = np.ones((3, 3)) + 0.25
hyst_kernel = torch.from_numpy(hyst_kernel).unsqueeze(0).unsqueeze(0)
hyst_kernel.requires_grad = False
with torch.no_grad():
self.conv4.weight = nn.Parameter(hyst_kernel)
# Threshold parameters
self.lowThreshold = torch.nn.Parameter(torch.tensor(0.10), requires_grad=True)
self.highThreshold = torch.nn.Parameter(torch.tensor(0.20), requires_grad=True)
def get_gaussian_kernel(self, k=3, mu=0, sigma=1, normalize=True):
# compute 1 dimension gaussian
gaussian_1D = np.linspace(-1, 1, k)
# compute a grid distance from center
x, y = np.meshgrid(gaussian_1D, gaussian_1D)
distance = (x ** 2 + y ** 2) ** 0.5
# compute the 2 dimension gaussian
gaussian_2D = np.exp(-(distance - mu) ** 2 / (2 * sigma ** 2))
gaussian_2D = gaussian_2D / (2 * np.pi * sigma ** 2)
# normalize part (mathematically)
if normalize:
gaussian_2D = gaussian_2D / np.sum(gaussian_2D)
return gaussian_2D
def get_sobel_kernel(self, k=3):
# get range
range = np.linspace(-(k // 2), k // 2, k)
# compute a grid the numerator and the axis-distances
x, y = np.meshgrid(range, range)
sobel_2D_numerator = x
sobel_2D_denominator = (x ** 2 + y ** 2)
sobel_2D_denominator[:, k // 2] = 1 # avoid division by zero
sobel_2D = sobel_2D_numerator / sobel_2D_denominator
return sobel_2D
def set_local_maxima(self, magnitude, pts, w_num, w_denum, row_slices,
col_slices, out):
"""Get the magnitudes shifted left to make a matrix of the points to
the right of pts. Similarly, shift left and down to get the points
to the top right of pts."""
pts = pts.cuda()
out = out.cuda()
r_0, r_1, r_2, r_3 = row_slices
c_0, c_1, c_2, c_3 = col_slices
c1 = magnitude[:,0,r_0, c_0][pts[:,0,r_1, c_1]]
c2 = magnitude[:,0,r_2, c_2][pts[:,0,r_3, c_3]]
m = magnitude[pts]
w = w_num[pts] / w_denum[pts]
c_plus = c2 * w + c1 * (1 - w) <= m
c_plus = c_plus.cuda()
c1 = magnitude[:,0,r_1, c_1][pts[:,0,r_0, c_0]]
c2 = magnitude[:,0,r_3, c_3][pts[:,0,r_2, c_2]]
c_minus = c2 * w + c1 * (1 - w) <= m
c_minus = c_minus.cuda()
out[pts] = c_plus & c_minus
return out
def get_local_maxima(self, isobel, jsobel, magnitude, eroded_mask):
"""Edge thinning by non-maximum suppression."""
abs_isobel = torch.abs(jsobel)
abs_jsobel = torch.abs(isobel)
eroded_mask = eroded_mask & (magnitude > 0)
# Normals' orientations
is_horizontal = eroded_mask & (abs_isobel >= abs_jsobel)
is_vertical = eroded_mask & (abs_isobel <= abs_jsobel)
is_up = (isobel >= 0)
is_down = (isobel <= 0)
is_right = (jsobel >= 0)
is_left = (jsobel <= 0)
#
# --------- Find local maxima --------------
#
# Assign each point to have a normal of 0-45 degrees, 45-90 degrees,
# 90-135 degrees and 135-180 degrees.
#
local_maxima = torch.zeros(magnitude.shape, dtype=bool)
# ----- 0 to 45 degrees ------
# Mix diagonal and horizontal
pts_plus = is_up & is_right
pts_minus = is_down & is_left
pts = ((pts_plus | pts_minus) & is_horizontal)
# Get the magnitudes shifted left to make a matrix of the points to the
# right of pts. Similarly, shift left and down to get the points to the
# top right of pts.
local_maxima = self.set_local_maxima(
magnitude, pts, abs_jsobel, abs_isobel,
[slice(1, None), slice(-1), slice(1, None), slice(-1)],
[slice(None), slice(None), slice(1, None), slice(-1)],
local_maxima)
# ----- 45 to 90 degrees ------
# Mix diagonal and vertical
#
pts = ((pts_plus | pts_minus) & is_vertical)
local_maxima = self.set_local_maxima(
magnitude, pts, abs_isobel, abs_jsobel,
[slice(None), slice(None), slice(1, None), slice(-1)],
[slice(1, None), slice(-1), slice(1, None), slice(-1)],
local_maxima)
# ----- 90 to 135 degrees ------
# Mix anti-diagonal and vertical
#
pts_plus = is_down & is_right
pts_minus = is_up & is_left
pts = ((pts_plus | pts_minus) & is_vertical)
local_maxima = self.set_local_maxima(
magnitude, pts, abs_isobel, abs_jsobel,
[slice(None), slice(None), slice(-1), slice(1, None)],
[slice(1, None), slice(-1), slice(1, None), slice(-1)],
local_maxima)
# ----- 135 to 180 degrees ------
# Mix anti-diagonal and anti-horizontal
#
pts = ((pts_plus | pts_minus) & is_horizontal)
local_maxima = self.set_local_maxima(
magnitude, pts, abs_jsobel, abs_isobel,
[slice(-1), slice(1, None), slice(-1), slice(1, None)],
[slice(None), slice(None), slice(1, None), slice(-1)],
local_maxima)
return local_maxima
def threshold(self, img):
""" Thresholds for defining weak and strong edge pixels """
alpha = 100000
weak = 0.5
strong = 1
res_strong = strong * (alpha * (img - self.highThreshold)).sigmoid()
res_weak_1 = weak * (alpha * (self.highThreshold - img)).sigmoid()
res_weak_2 = weak * (alpha * (self.lowThreshold - img)).sigmoid()
res_weak = res_weak_1 - res_weak_2
res = res_weak + res_strong
return res
def hysteresis(self,img):
# Create image that has strong pixels remain at one, weak pixels become zero
img_strong = img.clone()
img_strong[img == 0.5] = 0
# Create masked image that turns all weak pixel into ones, rest to zeros
masked_img = img.clone()
masked_img[torch.logical_not(img == 0.5)] = 0
masked_img[img == 0.5] = 1
# Calculate weak edges that are changed to strong edges
changed_edges = img.clone()
changed_edges[((self.conv4(img_strong) > 1) & (masked_img == 1))] = 1
# Add changed edges to already good edges
changed_edges[changed_edges!=1] = 0
# Add changed edges to already good edges
return changed_edges
def forward(self, x):
# Gaussian filter
x = self.conv1(x)
# Sobel filter
sobel_x = self.conv2(x)
sobel_y = self.conv3(x)
# Magnitude and angles
eps = 1e-10
self.grad_magnitude = torch.hypot(sobel_x + eps, sobel_y + eps)
# Non-max-suppression
eroded_mask = torch.ones((self.batch_size,1,256,256), dtype=bool).cuda()
eroded_mask[:, 0, :1, :] = 0
eroded_mask[:, 0, -1:, :] = 0
eroded_mask[:, 0, :, :1] = 0
eroded_mask[:, 0, :, -1:] = 0
thin_edges = self.get_local_maxima(sobel_x, sobel_y, self.grad_magnitude, eroded_mask)
thin_edges = self.grad_magnitude * (thin_edges * 1)
# Double threshold
thin_edges = thin_edges / torch.max(thin_edges)
thresh = self.threshold(thin_edges)
# Hysteresis
result = self.hysteresis(thresh)
return result
Train:
from model import Net
import numpy as np
from batch_generator import GenerateImageBatch
import torch
from torch.utils.tensorboard import SummaryWriter
writer = SummaryWriter()
def dice_loss(input, target):
smooth = 1.
iflat = input.view(-1)
tflat = target.view(-1)
intersection = (iflat * tflat).sum()
return (1 - ((2. * intersection + smooth) / (iflat.sum() + tflat.sum() + smooth)))
def main():
# Load data
train_images = np.load(r'path\train_image.npy')
train_labels = np.load(r'path\train_label.npy')
validation_images = train_images
validation_labels = train_labels
# Create batch architecture
batch_size = 1
epochs = 50
learning_rate = 0.00001
train_data = GenerateImageBatch(train_images, train_labels, batch_size)
validation_data = GenerateImageBatch(validation_images, validation_labels, batch_size)
# Create model object
net = Net(batch_size)
net.cuda()
net = net.float()
# Set up the optimizer, the loss, the learning rate scheduler and the loss scaling for AMP
optimizer = torch.optim.Adam(net.parameters(), lr=learning_rate)
criterion = dice_loss
# Begin training
for epoch in range(1, epochs+1):
net.train()
train_loss = 0
for i in range(int(train_data.img_count / batch_size)):
# Forward pass: Compute predicted y by passing x to the model
train_data.next_batch()
inputs = train_data.inputs
inputs.astype(np.float32)
inputs = np.transpose(inputs, (0, 3, 1, 2))
inputs = torch.from_numpy(inputs)
outputs = torch.from_numpy(train_data.outputs.astype(np.float32))
outputs = np.transpose(outputs.float(), (0, 3, 1, 2))
inputs, outputs = inputs.cuda(), outputs.cuda()
inputs = inputs.type(torch.float32)
outputs = outputs.type(torch.float32)
y_pred = net(inputs)
y_pred = y_pred.cuda()
# Compute and print loss
loss = criterion(y_pred, outputs)
writer.add_scalar("Loss/train", loss, epoch)
print('Loss:')
print(loss)
# Zero gradients, perform a backward pass, and update the weights.
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Calculate Loss
train_loss += loss.item()
net.eval()
valid_loss = 0
for i in range(int(validation_data.img_count / batch_size)):
validation_data.next_batch()
inputs = validation_data.inputs
inputs = np.transpose(inputs, (0, 3, 1, 2))
inputs.astype(np.float32)
inputs = torch.from_numpy(inputs)
outputs = torch.from_numpy(validation_data.outputs)
outputs = np.transpose(outputs, (0, 3, 1, 2))
inputs, outputs = inputs.cuda(), outputs.cuda()
inputs = inputs.type(torch.float32)
outputs = outputs.type(torch.float32)
y_pred = net(inputs)
# Compute and print loss
loss = criterion(y_pred, outputs)
writer.add_scalar("Loss/validate", loss, epoch)
valid_loss += loss.item()
print(f'Epoch {epoch} \t\t Training Loss: {train_loss / (int(train_data.img_count / batch_size))} \t\t Validation Loss: {valid_loss / (int(validation_data.img_count / batch_size))}')
print(f'Validation Loss {valid_loss:.6f}) \t Saving The Model')
# Saving State Dict
train = train_loss / (int(train_data.img_count / batch_size))
valid = valid_loss / (int(validation_data.img_count / batch_size))
torch.save(net.state_dict(), '../train_results/epoch_' + str(epoch) + '_train-loss_' + str(train) + '_val_loss_' + str(valid) + '.pth')
writer.flush()
writer.close()
if __name__ == "__main__":
main()
Single data-target pair.
Input image:

Label:
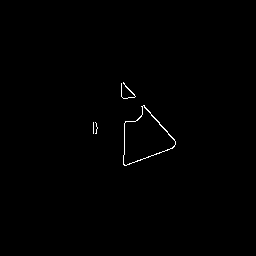
I am using PyTorch version 1.11.0