Filters and kernels are usually referring to the same object, but if I understand you correctly you are calling a 3D tensor a filter and each 2D slice a kernel?
If so, it seems you would like to get the activations after each “filter” was applied to the corresponding input activation channel and after the spatial dimensions (height and width) were already reduced, BUT before the channel dimension is reduced?
It would be possible to achieve this using grouped convolutions, but you would need to perform a lot of reshaping and would need to know how the conv kernels are applied internally.
For grouped convs, take a look at this post first as it gives you some information about the order the kernels are applied.
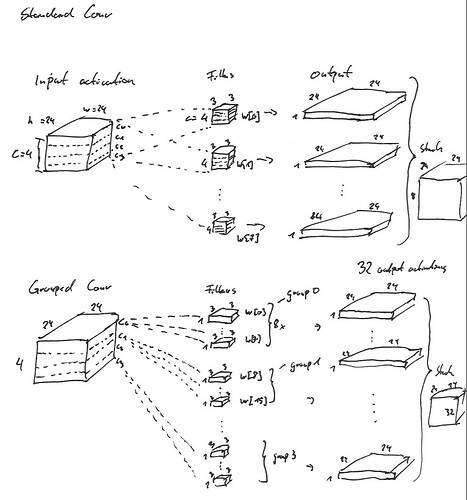
Let’s assume you are working with an input activation in the shape [batch_size=1, channels=4, height=24, width=24] and a standard conv layer with a weight tensor in the shape [out_channels=8, in_channels=4, height=3, width=3]. To keep the spatial dimension equal, let’s also use padding=1 and stride=1. Let’s also set the bias to None to make it a bit easier.
Now, you could use a grouped convolution via nn.Conv2d(4, 8*4, 3, 1, 1, groups=4), however you would need to be careful about the order how these filters are applied.
The main issue are the needed permutations needed in the filters as the grouped conv is applied sequentially on each input channel as seen in the linked post, while the standard conv applies a “full” kernel with all its channels to the input, so all input channels will be used on each filter.
It’s a bit hard to describe in words and although my drawing skills are not perfect, here is an illustration:
And here the corresponding code:
import torch
import torch.nn as nn
N, C, H, W = 1, 4, 24, 24
for _ in range(100):
N, C, H, W = torch.randint(1, 100, (4,))
x = torch.rand(N, C, H, W)
out_channels = 8
kw = 3
conv = nn.Conv2d(C, out_channels, kw, 1, 1, bias=False)
out = conv(x)
#print(out.shape)
# > torch.Size([1, 8, 24, 24])
conv_grouped = nn.Conv2d(C, C*out_channels, kw, 1, 1, groups=C, bias=False)
with torch.no_grad():
conv_grouped.weight.copy_(conv.weight.permute(1, 0, 2, 3).reshape(C*out_channels, 1, kw, kw))
out_grouped = conv_grouped(x)
#print(out_grouped.shape)
# > torch.Size([1, 32, 24, 24])
out_grouped = out_grouped.view(N, C, out_channels, H, W).permute(0, 2, 1, 3, 4).reshape(N, C*out_channels, H, W)
# manually reduce
idx = torch.arange(out_channels)
idx = torch.repeat_interleave(idx, C)
idx = idx[None, :, None, None].expand(N, -1, H, W)
out_grouped_reduced = torch.zeros_like(out)
out_grouped_reduced.scatter_add_(dim=1,index=idx, src=out_grouped)
# check error
print(torch.allclose(out_grouped_reduced, out, atol=5e-6), (out_grouped_reduced - out).abs().max())
As you can see, the outputs are equal after the “manual” reduction.
You could manipulate the pretrained VGG19 by replacing all conv layers with their grouped equivalent. I think writing a custom conv layer implementation would be beneficial given the complexity of the code.