Why 2D batch normalisation is used in features and 1D in classifiers?

vision
4

Hi

There is a universal BatchNorm!
Simply put here is the architecture (torch.nn.modules.batchnorm — PyTorch 1.11.0 documentation):

  1. a base class for normalization, either Instance or Batch normalization → class _NormBase(Module). This class includes no computation and does not implement def _check_input_dim(self, input)
  2. Now we have class _BatchNorm(_NormBase) that extends _NormBase which actually does the computation and tracks the values necessary for it. In the last line, you see that class calls return F.batch_norm(..) in its forward function. We will talk about F.batch_norm() in a bit.
  3. In the end, you have classes in form class BatchNormXd(_BatchNorm) that extend _BatchNorm and the only thing they do is to implement _check_input_dim(self, input) that was intentionally left behind in _NormBase class (see step 1).

About torch.nn.functional.batch_norm (from step 2): This function, does all the computation given values, in other words, if you want to mix all parts into a single class, you should be able too, but it would break the modularity, etc.

Here is an example that you can exactly replicate what BatchNormXd does for just a single forward pass given the normalization formulation:

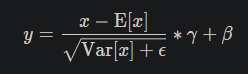
image

# Test case
x = torch.randn(2, 7)  # batch=2, features=7
running_mean = x.mean(dim=0)  # assuming 'mean' tracked during training
# Remark: as the documentation says, we must use biased estimator, i.e. 'unbiased=False'.
running_var = x.var(dim=0, unbiased=False)  # assuming 'var' tracked during training
gamma = None  # assuming 'gamma' is not set
beta = None  # assuming 'beta' is not set

>>> x
tensor([[ 1.6080,  1.5907, -1.0321,  1.0416, -0.8388,  0.0759, -0.9885],
        [-0.1404,  0.7668,  1.4246, -0.4341, -1.0590,  0.7760,  0.8207]])
		
# BatchNorm as a function
import torch.nn.functional as F

>>> F.batch_norm(x, running_mean, running_var, gamma, beta, momentum=0.)
tensor([[ 1.0000,  1.0000, -1.0000,  1.0000,  0.9996, -1.0000, -1.0000],
        [-1.0000, -1.0000,  1.0000, -1.0000, -0.9996,  1.0000,  1.0000]])


# BatchNorm as a class
import torch.nn as nn

bn1d = nn.BatchNorm1d(x.shape[1], affine=False, momentum=None)  # 'affine=False' sets beta and gamma to None
# you can verify mean and var by bn1d.running_mean and bn1d.running_var
# you can verify gamma and beta by bn1d.weight and bn1d.bias

>>> bn1d(x)
tensor([[ 1.0000,  1.0000, -1.0000,  1.0000,  0.9996, -1.0000, -1.0000],
        [-1.0000, -1.0000,  1.0000, -1.0000, -0.9996,  1.0000,  1.0000]])

Bests

4 Likes