Why dloss_dw.sum() and dloss_db.sum() in "Deep Learning with PyTorch"?

[oat]

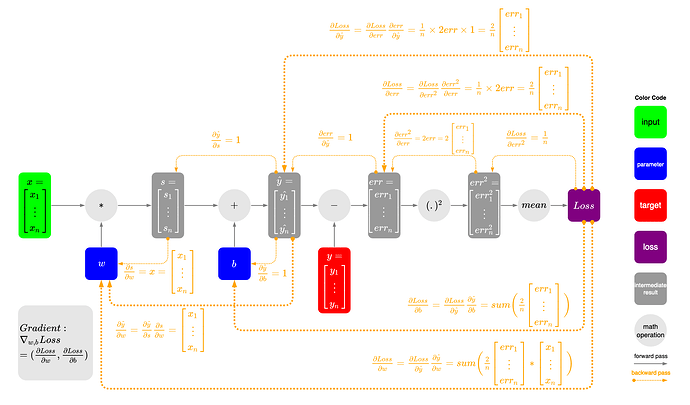
I’m reading “Deep Learning with PyTorch” by Eli Stevens, Luca Antiga, and Thomas Viehmann. As shown on page 116, the gradients for w and b are calculated as dloss_dw.sum() and dloss_db.sum().

Although the authors offered explanations, can you help to understand:

1. Why the element-wise multiplication between dloss_dtp and dmodel_dw, and that between dloss_dtp and dmodel_db?
2. Why the summation for dloss_dw and dloss_db, when returning the gradient vector?

I created a diagram as shown below to help myself to understand the vector calculations under the hood. However, I’m still not sure why the summation is applied in the last step. (x is t_u, y_hat is t_p, y is t_c in the book)

Thanks.

Excerpt from page 116 in “Deep Learning with PyTorch”:

My diagram on gradient calculation:

[tom (Thomas V)]

1. The elementwise multiplication is a radical simplification of the compute involved in the the chain rule. You could probably do something like dloss_dw = torch.diagonal_embedding(dmodel_dw(...)) @ dloss_dtp to be closer to the chain rule but less computationally efficient.
2. The summation is from using the same term multiple times, here from broadcasting. You can try this yourself on paper by spelling out the gradients per element (for two elements). Or you could have a simpler version with just some scalar g(x,y) and try to compute the derivative of f(x) = g(x,x) to see the same abstract principle.

Best regards

Thomas