Why do we need to set the gradients manually to zero in pytorch?

42

If you don’t specify other behavior (retain_graph=True or something like that) you are right.

43

As @justusschock said, the memory consumption is the same if neglecting overhead, but the graph structures are different. Illustrations are more clear:

%E6%9C%AA%E5%91%BD%E5%90%8D%E6%96%87%E4%BB%B6

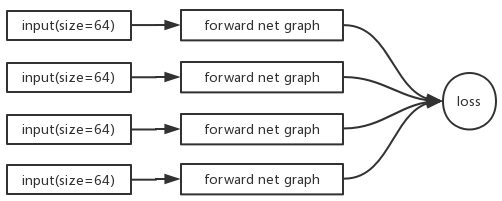
%E6%9C%AA%E5%91%BD%E5%90%8D%E6%96%87%E4%BB%B6%20(1)

AFAIK, graphs cannot be explicitly manipulated. Only indirect ways like backward and name scoping are available.

3 Likes
44

Thank you!
But why you mention

graphs cannot be explicitly manipulated

what are are explicitly manipulation or what do you imply?

45

Sorry for confusing. I just wanna say, the computation graph is created and freed automatically, behind the operations.
Understanding what happend to graph is helpful.

Maybe it’s a good idea to add a graph semantic section in the documentation, elaborating various cases involving.

46

Do I only need to divide by iter_size if the loss function takes the average ?
Let’s say if I’m doing sum of squared errors, should I call backward() without dividing loss by iter_size?

Also, do I also need to be worried about batch normalization in this case if I don’t divide by iter_size?
Thanks!

47

Do you mean we should not zero out gradients for RNN? I thought the cell state would be doing most of the work of remembering the information.

49

This looks like the main reason why the design decision is made not to remove the gradients.
What I was trying to understand isn’t it the best time to remove the gradients after the optimizer step.

The idea is we don’t need to track when a certain functions ends, we just track the optimizer.
However, I am uncertain if this logic fits all the use cases, such as GANs, but I would like to hear the opinions.

I actually think zeroing gradients can be a design decision (with default to zero them).

50

hi alban…
Thanks for your inputs above…
I am doing the grad accumulation using this way… could you please let me know if there is any problem here

total_loss=0.
        learn.model.train()
        for i,(xb,yb) in enumerate(learn.data.train_dl):
            #print('i',i)
            
            loss = learn.loss_func(learn.model(xb), yb)
            if (i+1) %2==0: # doing grad accumulation
              loss=total_loss*0.9+loss*0.1 # some loss smoothning
              #print('i',i)
              loss.backward()
              learn.opt.step()
              learn.opt.zero_grad()
              total_loss=0.
            else:
              total_loss+= loss # accumulate the loss
1 Like
51

Hi,

This looks good to me !

52

Hi,

It depends a lot on your usecase. sometimes you want to keep some gradients longer (to compute some statistics?).
But I agree that this is just a design decision. Unfortunately the original decision that was made was not to zero them and I don’t think we can change it now (for backward compatibility reasons).

1 Like
53

what if we don’t have an optimizer and just the model?

54

Is the accumulation of gradients the assumption that each time we do a backward pass we are including it from other loss functions or something and we are adding?

I don’t understand why accumulation is the operation to do with multiple backward passes.

55

why do we backpropagate through an RNN several times and therefore make accumulation justifiable? Why accumulation?

56

Is the total_loss need to be divided by 64 and batchsize ?

In my option, the batchsize is not needed, the loss function has done the mean to you, right?

1 Like
57

I think we don’t need to divide the batchsize and item_size in the loss1 += loss_2, as the loss is back alone there different graph_path. the loss plus here is not the iter_num. Right?

58

Thanks for your solution! I have a small question for your 2nd and 3rd methods.
For example, the batch size is set to 10, and I want the learning rate to be 1e-3, so do I have to mannually set the learning rate to 1e-3 / batch_size (1e-4 in this case)? Thanks!

59

It depends on what your loss is.
If it should be the average of the loss of all samples, you want to divide the final loss by the number of mini-batches you used.
If it should be the sum, then they will be the same as 1) already.

60

what do you mean that “RNNs are back propagated several times”? I’ve always considered RNNs as a long feedward net really, so we only back prop through it once like any other model…

61

Note sure what you mean by “accumulates gradients”. Calling backward twice is not even allowed without explicitly trying to do it. See trivial code and errors:

import torch

w = torch.tensor([4.0], requires_grad=True)

l = (w - 1.0)**2
l.backward()

print('---1st backard call---')
print(w.grad)
print()

print('---2nd backward call---')
l.backward()

errors:

python backward_pass_twice.py
---1st backard call---
tensor([6.])

---2nd backward call---
Traceback (most recent call last):
  File "backward_pass_twice.py", line 13, in <module>
    l.backward()
  File "/Users/me/miniconda3/envs/ml/lib/python3.7/site-packages/torch/tensor.py", line 166, in backward
    torch.autograd.backward(self, gradient, retain_graph, create_graph)
  File "/Users/me/miniconda3/envs/ml/lib/python3.7/site-packages/torch/autograd/__init__.py", line 99, in backward
    allow_unreachable=True)  # allow_unreachable flag
RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed. Specify retain_graph=True when calling backward the first time.
62

Excellent example! Thank you.

But why did you not need to call retain_graph=True?