A question about F.conv2d

autograd
1

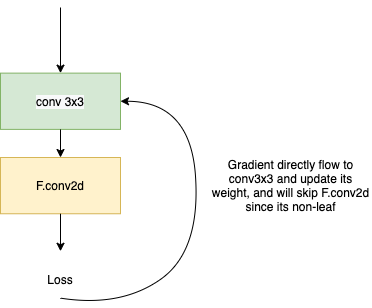
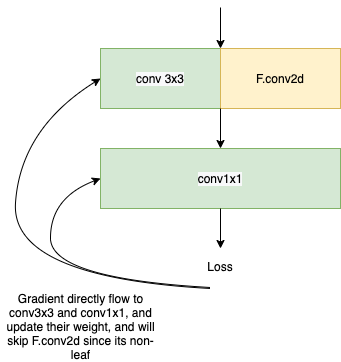
Below is a simple reproducible code snippet:
I know this might be a simple question, but I never thought of it before and just want to confirm here.

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        
        self.conv = nn.Conv2d(1,1,3, padding=1, bias=False)
        self.weight1 = self.conv.weight * 10
        
    def forward(self, x):

        out = self.conv(x)
        out2 = F.conv2d(out, self.weight1, padding=1)

        return out2

then during back-propagation, I noticed that self.weight1 will not be updated.

net = Net()
# -> checkpoint 1: print(net.conv1.weight, net.weight1)
optimizer1 = optim.SGD(net.parameters(), lr=0.001)
Loss1 = nn.L1Loss()

k = torch.ones((1,1,5,5))
gt = torch.zeros((1,1,5,5))

# back propagation
optimizer1.zero_grad()

pred = net(k)
loss1 = Loss1(gt, pred)

loss1.backward()
optimizer1.step()
# -> checkpoint 2: print(net.conv1.weight, net.weight1)

for the above 2 checkpoints, the outputs are below:

# checkpoint 1: print(net.conv1.weight, net.weight1)
Parameter containing:
tensor([[[[ 0.1280,  0.1039, -0.1972],
          [-0.2293,  0.1194, -0.1370],
          [-0.3182, -0.1437,  0.0395]]]], requires_grad=True) 
tensor([[[[ 1.2796,  1.0391, -1.9720],
          [-2.2928,  1.1938, -1.3697],
          [-3.1816, -1.4372,  0.3954]]]], grad_fn=<MulBackward0>)

# checkpoint 2: print(net.conv1.weight, net.weight1)
Parameter containing:
tensor([[[[ 0.1337,  0.1111, -0.1900],
          [-0.2223,  0.1278, -0.1290],
          [-0.3123, -0.1371,  0.0456]]]], requires_grad=True) 
tensor([[[[ 1.2796,  1.0391, -1.9720],
          [-2.2928,  1.1938, -1.3697],
          [-3.1816, -1.4372,  0.3954]]]], grad_fn=<MulBackward0>)

you can see self.weight1 in network does not get updated. but self.weight1 is a torch.tensor and it has a gradient, i.e. net.weight1.requires_grad is True. This is because self.weight1 is a non-leaf tensor.

This is not my confusion, my question is, since self.weight1 is not get updated, does that mean, the gradients from loss directly propagate to self.conv, because the layer F.conv is not learning(i.e. because F.conv is not part of the graph)?

Really appreciate if anyone can give me some hints.

2

Hi,

To make sure that a Module attribute is recognized as a learnable parameter, it needs to be wrapped in the nn.Parameter.
As you code is today, weight1 won’t actually appear in net.parameters() and so the optimizer won’t know about it.

Also for the .grad field of a Tensor to be populated, you want to make sure that it is a leaf Tensor (it has no history). Right now, because weight1 is computed based on conv.weight, it is not a leaf (you can check .is_leaf()).
You can detach it from its history to force it to be a leaf. So the updated code is:
self.weight1 = nn.Parameter((self.conv.weight * 10).detach())

3

Hi @albanD,

Thanks for your reply! Its really clear and helpful.
Yes I understand that we need to use nn.Parameter to wrap the weight.
But here I want to know a bit more about what will happen to gradient flow if we intentionally let it be a non-leaf component.

So for the code I shared above, does it mean that the gradient from Loss will directly flow to self.conv1 and F.conv2d there is just like an operator outside the network(since its non-leaf)?

And in general, can I assert like below?
for connection in series:
st1
for connection in parallel(torch.cat()):
st2

Really thanks for your time and help!

4

Hi,

If you leave it as your first example, when you backprop the F.conv2d, no gradient get accumulated since no input is a leaf.
But then you backprop through the computation of self.weight1 and that will add gradients to self.conv.weight.
In parallel, you backprop through self.conv which will also accumulate gradients into self.conv.weight.
So in the end, the gradients in self.conv.weight is just the sum of the gradients of all the places where it is used.

5

Hi @albanD,

Thanks for the answer! Appreciate.