Hello All,
I am running multi-label segmentation of 3D data(batch x classes x H x W x D). The target is 1-hot encoded[all 0s and 1s].
I have broad questions about the loss to be used.
In V-net paper: https://arxiv.org/pdf/1606.04797.pdf
The dice loss used as:
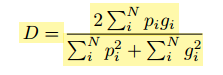
which varies from 0~1, and intended to maximize. Like regular IoU/Dice.
In Generalized dice paper: https://arxiv.org/pdf/1707.03237.pdf
GDL loss is:
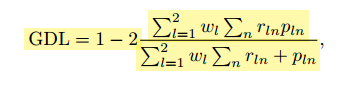
and the author says about the weight:
when choosing the GDLv weighting, the contribution of each label is
corrected by the inverse of its volume, thus reducing the well-known correlation
between region size and Dice score
which I understand very well.
So, when I implement both losses with the following code from: pytorch/torch/nn/functional.py at rogertrullo-dice_loss · rogertrullo/pytorch · GitHub
torch.manual_seed(1001)
out = Variable(torch.randn(3, 9, 64, 64, 64))
print >> tensor(5.2134) tensor(-5.4812)
seg = Variable(torch.randint(0,2,[3,9,64,64, 64])) #target is in 1-hot-encoded format
def dice_loss(prediction, target, epsilon=1e-6):
"""
prediction is a torch variable of size BatchxnclassesxHxW representing log probabilities for each class
target is a 1-hot representation of the groundtruth, shoud have same size as the prediction
"""
assert prediction.size() == target.size(), "prediction sizes must be equal."
assert prediction.dim() == 5, "prediction must be a 4D Tensor."
uniques = np.unique(target.numpy())
assert set(list(uniques)) <= set([0, 1]), "target must only contain zeros and ones"
probs = F.softmax(prediction, dim=1) # channel/classwise
num = probs * target # b,c,h,w--p*g
num = torch.sum(num, dim=4)
num = torch.sum(num, dim=3)
num = torch.sum(num, dim=2) # b,c
den1 = probs * probs # --p^2
den1 = torch.sum(den1, dim=4) #b,c,h
den1 = torch.sum(den1, dim=3) #b,c,h
den1 = torch.sum(den1, dim=2)
den2 = target * target # --g^2
den2 = torch.sum(den2, dim=4)
den2 = torch.sum(den2, dim=3)
den2 = torch.sum(den2, dim=2)
den = (den1+den2+epsilon)#.clamp(min=epsilon)
dice=2*(num/den)
dice_eso=dice #[:,1:]#we ignore background dice val, and take the foreground
dice_total=torch.sum(dice_eso)/dice_eso.size(0)#divide by batch_sz
return dice_total
dice_loss(prediction=out, target=seg)
I get a dice score of 1.9096 why is it beyond 1 and when using it as loss criterion during training, what limit it has to be maximized?
And when using GDL from: pytorch-3dunet/pytorch3dunet/unet3d/losses.py at eafaa5f830eebfb6dbc4e570d1a4c6b6e25f2a1e · wolny/pytorch-3dunet · GitHub
class GeneralizedDiceLoss(_AbstractDiceLoss):
"""Computes Generalized Dice Loss (GDL) as described in https://arxiv.org/pdf/1707.03237.pdf.
"""
def __init__(self, normalization='sigmoid', epsilon=1e-6):
super().__init__(weight=None, normalization=normalization)
self.epsilon = epsilon
def dice(self, prediction, target, weight):
assert prediction.size() == target.size(), "'prediction' and 'target' must have the same shape"
prediction = flatten(prediction) #flatten all dimensions except channel/class
target = flatten(target)
target = target.float()
if prediction.size(0) == 1:
# for GDL to make sense we need at least 2 channels (see https://arxiv.org/pdf/1707.03237.pdf)
# put foreground and background voxels in separate channels
prediction = torch.cat((prediction, 1 - prediction), dim=0)
target = torch.cat((target, 1 - target), dim=0)
w_l = target.sum(-1)
w_l = 1 / (w_l * w_l).clamp(min=self.epsilon)
w_l.requires_grad = False
intersect = (prediction * target).sum(-1)
print(intersect.shape)
intersect = intersect * w_l
denominator = (prediction + target).sum(-1)
print(denominator)
denominator = (denominator * w_l).clamp(min=self.epsilon)
return 1 - (2 * (intersect.sum() / denominator.sum()))
GeneralizedDiceLoss(normalization='softmax').dice(prediction=out, target=seg, weight=None)
I get a dice score with the same 1.0013
Though I don’t know how GDL varies compared to the V-net Dice but can they be compared to some extent in terms of optimization?
Also, how do I use this in training?
For example,
img, seg = img.to(device), seg.to(device)
out = model(img)
optimizer.zero_grad()
loss = dice_loss_3d(out, seg).cuda()
# print(loss)
loss.backward()
optimizer.step()
running_loss += loss.item()
should work?