Hello there,
I need and trying to normalize my input using minmax normalization. I know this easily can be done with:
X_norm = (X - X.min() ) / ( X.max() - X.min())
But I also want to add learnable parameters to it like (assume register_parameter etc. already handled in init):
X_norm = ( X - X.min() ) / ( X.max() - X.min() ) * self.weight + self.bias
I am asking two things:
Is there already a built-in wrapper in pytorch that does this?
How much does it make sense to do it in terms of gradients? The differentiation would work well?
Using your first equation, we get values between [0, 1].
However, with the learnable parameters self.weight and self.bias this will not always be true. The values can be shifted and scaled.
Assuming you do not care about this. The you can use the BatchNorm2d (or 1d or 3d depending on your case).
As you can see, the equation is given as.
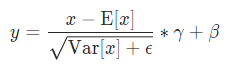
Where gamma and beta are your learnable parameters. The only difference to your original equation is that the mean is centered towards 0 and the division by the standard deviation will give you values between [-1, 1]. Instead of just resizing the values between [0, 1] without looking at the mean or std.
You can have values greater than 1 and lower than -1, but these will be mostly outliers.
In your implementation it will be prone to noise. This means that if you have one single outlier that is much greater than every other value, then the main information will be crammed together, in order to fit this value.
I think this would be a more robust solution.
Hope this helps