Hi i’m trying to use Optimal transport’s Wasserstein distance in pytorch.Before I had known about Geomloss (Getting started — GeomLoss) and their pytorch implementation of an approximation of it , I tried using the exact wasserstein distance on each predicted vector in a batch . “output[0]” represents the predicted batched and “tg” being the target being approximated .
reading Adding a float variable as an additional loss term works? I understand that adding constants(in that batch) gives a gradient of 0 so it should not affect back propogation whatsover but for me it does!
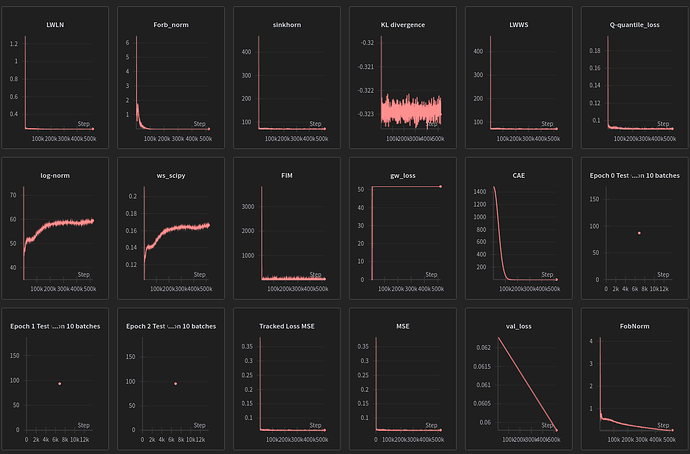
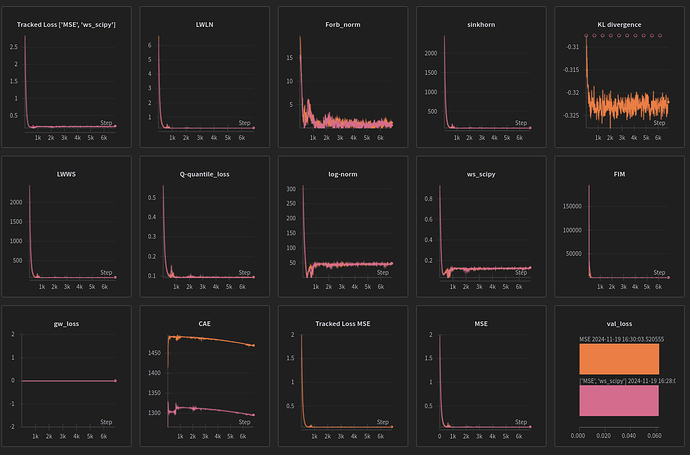
A model trained to do regression with MSE alone is being out performed MSE+Scipy’s WS implementation , in fact this combination is even better than the sinkhorn approximation+MSE combo by a notable margin later down the road .
MSE+ws_scipy can be used in loss.backward() and accelerator.backward(loss) but if u use ws_scipy alone things break because there is no graph behind it telling where to send the gradients to .pure MSE obviously doesn’t have this limitation.
My explination on this is that scipy’s term doesn’t create gradients but it’s presence increases MSE norm and that even in small variation(it’s own gradients alone couple with a big norm) is propagating WS information when it shouldn’t
an analogy is that I imagine the losses being partners .Each has a gradient (money) and a graph of norms(describing where to invest that money at) . Somehow in this combination WS has no money(not derivable by pytorch) and should therefore have no say in things but by injecting it’s norm in MSE’s graph it’s implifying MSE decision by increasing the norm sent through MSE’s graph alone .
if for neurone #250 it’s decided MSE small error , WS big error . WS shouldn’t affect the learning of it and should fall flat on it’s own but it’s somehow affecting MSE’s decision and sending big error still
here is code that shouldn’t work but does and outperforms MSE criterion alone
@ptrblck my hero in shining armor show me the way of the graphs (that we shouldn’t detach)
vec1_np = output[0].detach().cpu().numpy()
vec2_np = tg.detach().cpu().numpy()
# Compute Wasserstein distance for each pair of vectors
wsd_list = [wasserstein_distance(vec1_np[i], vec2_np[i]) for i in range(vec1_np.shape[0])]
# If you need an aggregate measure, you can compute the average distance
average_wsd = sum(wsd_list) / len(wsd_list)
loss_tr = criterion(output[0],tg)+average_wsd
accelerator.backward(loss_tr)
[figure of MSE+ws_scipy being significantly different despite running on the same seed]
seed=74
torch.manual_seed(seed)
np.random.seed(seed)
random.seed(seed)
here’s my github for this GitHub - AymenTlili131/Federated-Continual-learning-: PFE
Any help is appreciated before I crack open both libraries and start comparing implementations, I’d like to hear the opinions of people who contributed to them
scipy==1.12.0
torch==1.12.1+cu113 (on RTX 3060 ubuntu22)
torch_geometric==2.4.0
torchaudio==0.12.1
torchdata==0.5.1
torcheval==0.0.7
accelerate==0.30.1