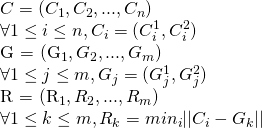Anyway to parallelize this function?

1 
def grid_minimal_dist(centroids,grids):
    r"""
    Get the minimal distance for each point
    in the grid to a centroid
    """
    # Number of sample
    t = centroids.size()[0]

    res = []
    for c,g in zip(centroids,grids):
        # Number of centroids
        n = c.size()[0]

        # Number of grid point
        m = g.size()[0]

        # Match the size of centroids and grid point
        c = c.repeat(m,1)
        g = g.repeat_interleave(n,dim=0)

        # Compute the L2 norm
        distance = g - c
        distance = distance.pow(2)
        distance = torch.sum(distance,1)
        distance = torch.sqrt(distance)

        # Regroup for each point of the grid
        distance = distance.view(m,n)

        # Get the minimal distance
        distance,_ = torch.min(distance,1)

        # Append the result
        res.append(distance)

    res = torch.stack(res)

    return res

Let us note t the number of samples.

centroids is a collection (list, tuple, etc. ) of t matrix (n,2), n is the same as in the code

Example : centroids = [ [ [1,0], [0,2] ], [ [0,0] ] ]

grids is a (t,m,2) tensor. There are t grids of m points in a 2 dimensional space.

The purpose of this function is to compute the distance of the nearest centroids for each point in grids.

So, if we take 1 take centroid matrix [[[1,0],[0,2]]] and a grid [[[0,0]]].

In this example, k = 1, m = 1, n = 2

We want to compute the result vectorof length m (the size of the grid). The result in this case will be

res = [[1]]

Because the nearest point to (0,0) was (1,0) and their L2 norm is 1.

This is done inside the for loop.

Now I would like to parallelize this, so t can be as great as 1000 for example.

The only problem to using only element wise operation is because of n, as it may varies for each value of t. Therefore, centroids cannot be a tensor (unless by using a mask perhaps?)

Sorry if this is confusing. Please ask any question for clarification purposes.

Best,

2

I don’t know if I got the point of your function, but as far as I understood, I think you can do the following:

import torch

def grid_minimal_dist(centroids, grids):
  z = (centroids[:, None, None, :] - grids).norm(dim=3)
  return z.min(0)[0].min(0)[0]

centroids = torch.Tensor([  [1,0], [0,2] ,  [0,0]  ])
grids = torch.Tensor([[[0,0]]])

print(grid_minimal_dist(centroids, grids))

n = 3
t = 4
m = 5
centroids = torch.rand(n, 2)
grids = torch.rand(t, m, 2)

print(grid_minimal_dist(centroids, grids))

Is it what you wanted ?

3

Thanks for your answer.

Let’s note a function named g. g takes as input two tensors : centroid which is of size (n,2) and grid which is of size (m,2)

g will return a size (m) tensor called ‘res’ for which each value of ‘res’ is the distance of the nearest point for each point in the grid to all centroids

image

And that is done inside the for loop.

The for loop is there because ideally I’d like to take multiple grids and multiple centroids and use element wise operation to make the computation quick. There number of multiple grids and multiple centroids is denoted by t.

In your example, centroids would be

centroids = torch.rand(t,n,2)

But the problem is that n may vary for each t, so I think centroids must be a list of tensors, or find a way to use a mask somehow so that the function knows how many centroids it has to deal with.

Sorry if it’s still confusing…

4

Thanks, I think I got it better now. You can always repeat on centroid, say the last one, in order to stack all centroids into one single tensor. You just need to take n as the max size of the centroids for all t. The snippet above can be easily adapted to this case. I guess the desired output should be of the shape (t, m), is that right ?