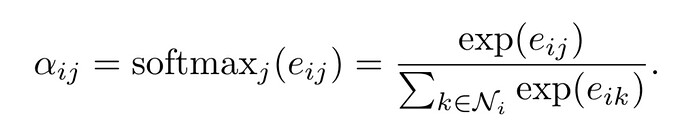Apply mask softmax

1

Hi everyone,

I try to implement the following function:

image
image1014×196 24.5 KB

At this stage, I have e.g. a tensor [[1,0,3], [0, 1, 2], [3, 2, 1]] and the softmax should be done for only values greater than 0 (neighbors), thus [[0.12, 0, 0.88], [0, 0.27, 0.73], [0.66, 0.24, 0.1]].

Is there an existing method to do this or does anyone have an idea ?

Thank you for your help !

1 Like
2

To clarify: you want to calculate the standard softmax BUT you want to ignore any zero values.

In other words for the first row you remove the zero, then you calculatesoftmax([1,3]), and then you reinsert the zero into the output.

Is that right?

If so, I am stumped. Maybe someone else can help.

3

Yes exactly ! The zeros have been obtained using torch.where.

4

I thought about using -10^10 instead of 0 for the soft max but there should be a better way I guess

2 Likes
5

I think that is a great idea. Anything else would require funny indexing and would probably end up being super inefficient.

6

Hi Diego. Does this approach work well?

7

Hi Andy-jqa

Yes absolutely !

8

Thanks for the reply.
I did something like this:

# matrix A is the one you want to do mask softmax at dim=1
A_max = torch.max(A,dim=1,keepdim=True)[0]
A_exp = torch.exp(A-A_max)
A_exp = A_exp * (A == 0).type(torch.FloatTensor) # this step masks
A_softmax = A_exp / torch.sum(A_exp,dim=1,keepdim=True)

which also seems to work.

4 Likes
9

Instead of .type(torch.FloatTensor) which will move the data to CPU if it was on the GPU, I would do .float() which will convert it while leaving it on the device it was on, as well as being shorter to type and easier to read.

1 Like
10

Great advice! Thanks.

11

In case you cannot make any assumptions about your data, you could use float('-inf')

4 Likes
12

Thanks a lot!
And I have a little suggestion:
A_softmax = A_exp /(torch.sum(A_exp,dim=1,keepdim=True)+epsilon)
It can avoid division by zero zero.

1 Like
13

I had to implement something similar. My approach was the following (where mask is a tensor of 1s and 0s indicating the entries to be removed):

def masked_softmax(vec, mask, dim=1):
    masked_vec = vec * mask.float()
    max_vec = torch.max(masked_vec, dim=dim, keepdim=True)[0]
    exps = torch.exp(masked_vec-max_vec)
    masked_exps = exps * mask.float()
    masked_sums = masked_exps.sum(dim, keepdim=True)
    zeros=(masked_sums == 0)
    masked_sums += zeros.float()
    return masked_exps/masked_sums
4 Likes
14

Thanks for your solution. But why do you need to compute zeros and add them to the masked_sums? Without zeros, pytorch can still compute the probability by broadcasting the masked_sums.

15

I wrote even simpler version:

def masked_softmax(vec, mask, dim=1, epsilon=1e-5):
    exps = torch.exp(vec)
    masked_exps = exps * mask.float()
    masked_sums = masked_exps.sum(dim, keepdim=True) + epsilon
    return (masked_exps/masked_sums)
4 Likes
16

ehn… directly feed vectors with float('-inf') to pytorch’s default nn.Softmax in fact returns nan at the entries with negative infty.

2 Likes
17

There is no need to add the epsilon as exp(x) is always larger than 0.

18

Try this

tsr = torch.Tensor([[1,0,3], [0, 1, 2], [3, 2, 1]]).float()
mask = ((tsr  > 0).float() - 1) * 9999  # for -inf
result = (tsr + mask).softmax(dim=-1)
1 Like
19

Here is a solution by filling masked placed with float(’-inf’):

import torch.nn.functional as F
F.softmax(vec.masked_fill((1 - mask).bool(), float('-inf')), dim=1)
1 Like
20

What is the logic behind skipping zeroes? Does it improve predictions?

1 Like