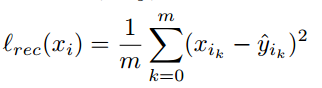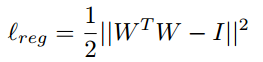Hello community,
I need to implement an autoencoder network described in this article https://arxiv.org/pdf/1803.09065. The model is very simple. Contains only a hidden layer, which corresponds to a binarization layer of the input code. My whole difficulty is the activation function used in the hidden layer is non-differentiable and therefore the same weight matrix of the output layer is used to update the input layer. I would like to know how I can do an activation function in pytorch that does not need to be derived and that uses the output layer weight matrix to update the weights of the input layer. I will be very grateful if anyone can help me.
The network architecture follows below.

1 Like
Could you explain it a bit?
Would you like to use the same gradients from the output layer on your input layer or copy the weights into the input layer after each update?
Hi @ptrblck,
I would like to copy the weights into the input layer after each update of the output layer.
Thanks for the information!
In that case this code example might work.
I tried to come up with a similar model architecture, so I just used three linear layers and had to transpose the weight matrix since I used a “bottleneck” layer.
Also, I call x.detach() after the first linear layer to fake your behavior of the gradient loss in the input layer:
class MyModel(nn.Module):
def __init__(self):
super(MyModel, self).__init__()
self.fc1 = nn.Linear(10, 5)
self.fc2 = nn.Linear(5, 5)
self.fc3 = nn.Linear(5, 10)
def forward(self, x):
x = F.relu(self.fc1(x))
x = x.detach() # Fake your use case so that fc1 cannot be updated
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
data = torch.randn(10, 10)
target = torch.randn(10, 10)
model = MyModel()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-3)
for epoch in range(10):
optimizer.zero_grad()
output = model(data)
loss = criterion(output, target)
loss.backward()
# print(model.fc1.weight.grad) # Will be None
optimizer.step()
print('Epoch {}, loss {}'.format(epoch, loss.item()))
# Copy weights from output layer to input layer
with torch.no_grad():
model.fc1.weight.copy_(model.fc3.weight.t())
Let me know, if this helps or if I misunderstood your use case.
1 Like
Hi @ptrblck,
Thank you. I’ll test and say if it worked 
Hi @ptrblck,
It worked! Thank you! I have another question =]. I need to use a heaviside (step) function from the input to the hidden layer, instead of the relu function applied here (x = F.relu (self.fc1 (x))), so that the values of this layer are binary [0,1]. I’ve seen that it has the heaviside function in numpy, but it’s conflicting with the pytorch because of the type. Any idea?
What kind of type issue do you see?
I would have to do something like this:
def forward(self, x):
x = np.heaviside(self.fc1(x),1)
x = x.detach()
x = F.tanh(self.fc2(x))
x = self.fc3(x)
return x
This error appears:
RuntimeError: Can’t call numpy() on Variable that requires grad. Use var.detach().numpy() instead.
You could probably indeed detach the output of fc1, since you won’t calculate gradients for it.
x = np.heaviside(self.fc1(x).detach().numpy(), 0)
x = torch.from_numpy(x)
Alternatively, you could also implement np.heaviside in PyTorch.
This worked \o/. Thank you 
Hi @ptrblck,
I would like to take one last doubt if possible.
This model uses a loss function that is the sum of two terms that follow.
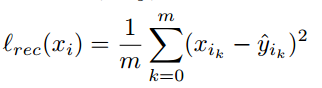
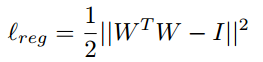
In the second term, W is the weight matrix and I is an identity matrix.
For both functions I have used MSELoss to implement. I tried the following.
loss = criterion_1(output, target) + criterion_2(torch.mm(model.fc3.weight,model.fc3.weight.t()), Variable((torch.eye(10))))
It did not make any error, but I was in doubt if the code is actually doing what is described in the two functions of the model.
I’m not sure how W and the matrix norm are defined in the paper.
If they are using the Frobenius norm, you cannot use nn.MSELoss:
w = torch.matmul(model.fc3.weight.t(),model.fc3.weight)
i = torch.eye(w.size(0))
# Frobenius norm
0.5 * (w - i).norm(p=2)
((w - i)**2).sum()**0.5 * 0.5
# MSE
criterion = nn.MSELoss()
criterion(w, i)
((w - i)**2).mean()
But as I said, I’m not familiar with the paper so I might misunderstand the notation.
The first loss looks alright.
Thanks for the explanation.
In the papers this notation is usually a norm L2 squared. In that case, I cannot use MSELoss, right?
Are there any other pytorch functions that I could use in this case?
Would my first approach work? (.norm(p=2))
Yes! In the paper, the authors did not specify the norm, but the L2 norm is usually used.
Sorry, I feel a little confused now. How would the norm be applied to the activation function?
I’m a bit confused, too.
Which activation function do you mean and what would you like to do with this function?
Based on the formula and code you’ve posted, it seems that l_reg is calculated based on the weight matrix of the last linear layer.
Sorry. I wrote wrong, I meant loss function and no activation function. The loss function I want to implement is made up of the two functions mentioned above. Would it be this?
loss = criterion(output, target) + 0.5*(w - i).norm(p=2)
I think this might work, but you should really check it with someone having more insight into the paper (or the general approach). 
1 Like
Really thank you for help!!!