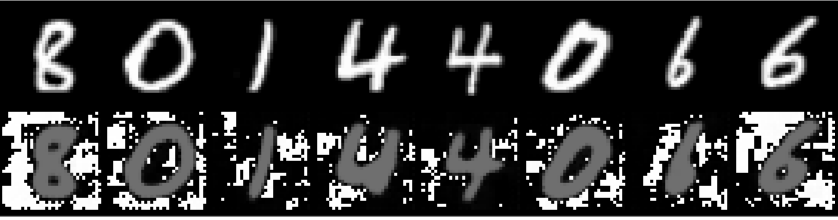Autoencoder: Reconstructed images incorrect after denormalization

vision
1

Hello there,
I am currently dealing with image reconstruction using a simple Convolutional Autoencoder. The Autoencoder is split into two networks:

  1. The Encoder: Maps the input image to latent space with ReLU as last activation function
  2. The Decoder: Maps the latent variable back to the image space. Last activation function is tanh or sigmoid.

The data preprocessing step is: [transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))] The mean and std values were calculated channel wise on the training set.
To denormalize/ unnormalize the images, I used the following code which is closely related to Unnormalize images:

def denormalize(data, mean, std):
data_un = data.new(*data.size())
n_channel = data.shape[1]
for c in n_channel:
data_un[:,c] = data[:,c]*std[c] + mean[c]
return data_un

When I train the network (with MSE loss on MNIST) and look at the reconstructed images they do not match, although the general structure looks very similar. Note that as activation functions in the final layer of the decoder, I tried both: sigmoid and tanh. After the normalization step of the input data, the images are shifted, so that they are in [-1,1]. For that reason, I thought it would make more sense to use an Tanh instead of a Sigmoid. However, when I denormalize the reconstructed images, they look off.
The first figure shows the sigmoid example, the latter figure displays the tanh example.
Note that, the first row shows the input images after they have been normalized and unnormalized, the second row shows the same images after reconstruction and unormalization.
Sigmoid:

img_grid_sigmoid_26
img_grid_sigmoid_26847×222 15 KB

Tanh:
img_grid_tanh_26
img_grid_tanh_26838×220 24.9 KB

The code below was used to log the images to Tensorboard:
dec_out: decoder output
data_nm: the normalized images given as input to the encoder
images_normalized = torch.concat([data_nm[:8, ].detach(), dec_out[:8, ].detach()])
images_unnormalized = denormalize(data=images_normalized, mean=(0.1307,), std=(0.3081,))
img_grid = make_grid(images_unnormalized, nows=8)

Do you have any idea why this happens and whether it is a good idea to denormalize the reconstructed images? Does it make sense to scale the input images after normalization back to [0,1]? Or is there something else that I am missing?
Thank you for any hints :slight_smile:

2

Instead of Tanh or Sigmoid or data mean and std to denorm the image, I would suggest using output’s min and max to denorm them

max = np.max(img)
min = np.min(img)
denormed_img = (img - min) / (max - min) * 255.0

3

Thank your for answering. So, would you make the last layer linear and then apply your above mentioned way? Please elaborate on your answer and your thoughts behind it.

4

Sigmoid scales the data between 0 and 1
Tanh scales the data between -1 and 1
The mean and std of the image are fine to scale the data as input but the output should be scaled the same way as your input to the loss.
I guess what I’m trying to explain (very badly) is that when you calculate the loss between the input image and output image, the network should be able to give in output in the same range as the input.
I would scale the input images between -1 and 1, use linear or tanh as layer of the network, and compute loss between input and output (both should be in -1 to 1 range now)
To visualize you can use the formula shared earlier

5

This was a great hint, thank you ! Maybe a quick update from my side and a few clearifications:

  1. Wrongfully, I didn’t check the range over the dataset after the normalization step: the real range is in [~-0.42, ~2.82].
  2. I tried unnormalizing the images with the formula that you have provided and it works fine. Now, I individually scale every image by its min and max.The images that I get look very similar, although a bit brighter then the originals. It is not required to scale them back to [0, 255] because (in my case) tensorboard can handle ranges in [0,1].
  3. So you would not normalize the data, so that is has 0 mean and an std of 1; rather rescale it?
6

As per my understanding, the basis for scaling comes from two reasons
a) when you have data from different types eg house prices, house areas, and the number of rooms, you want all the information in the same range. In such a case 0 mean std 1 makes sense because you don’t have a bound or range of data (or rather multiple ranges for each type of data)
b) you want to scale the images in a small range so that the network does not have to deal with large numbers (avoid exploding gradients) for stability.

When it comes to images I have seen people scale the data 0 to 1, -1 to 1, 0 mean std 1, or use the image net mean and std to scale the data. All of the approaches work fine in different cases.

To me, it seemed intuitive that you want to scale the output of the network to occupy the max range of color space (0-255) for best-looking results.

I know that’s not the exact answer to why, but hopefully gives you some insights into normalization

7

rescaling and normalization can be the same if you use the right mean and std :stuck_out_tongue:

8

Thanks. I mostly worked in domains where the algorithms had the explicit assumption that the mean and std are 0,1, respectively. IMHO using the imagenet values is a bit misleading because it works fine for most mondane domains but leaves out custom or highly specific datasets.

9

I agree, I have trained a single network on a mix of thermal and visible images, I found that calculating the mean and std over both modalities gave me the best results.