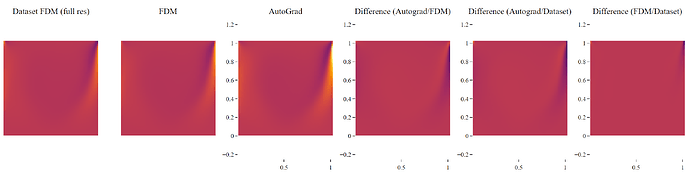
I am currently Experimenting with a Transformer Class Neural Operator and am seeing a bit of an error. When I calculate the gradient of the output for example dv/dx using traditional Finite Difference Method (FDM) and compare the same gradient output to the AutoGrad, they are similar but not quite there. Comparing to the FDM method on the underlying dataset too…
…shows that the Auto-grad is a bit off. The dataset also reached grid convergence so a 2nd order FDM can be considered ground truth, where the FDM method on the model is more accurate as seen in the last picture.
The only thing I can think of is that both the input and the output to the model are unit normalized (separately, not the same std, mean). However, based on my maths, that would mean that the gradients can be unnormalized by a combination of the std (my chain rule logic could be wrong here). However, the Autograd output is not a mulitple of the FDM output, meaning that multiplying the output by some combination of std won’t align the methods.
Due to the complexities of autograd, I am unable to calculate the same method but for a non-normalized input. Unless I include the normalization within the model, is this really the only option for further comparison or is there more complex things at play here between input queries and keys of cross attention?
If I understand correctly, you computed gradient of model w/o normalization using FDM.
The chain rule implies that autograd output is a linear function of FDM output, but its not necessarily a multiple.
To take into account the normalization, you could you could recompute just the normalization.
Then do torch.autograd.grad(input_after_norm, inputs=(input_before_norm,), grad_output=(fdm_output,))
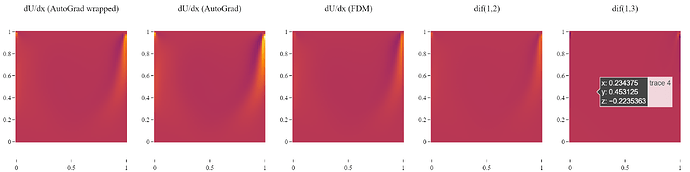
Yep, so I made the adjustment by wrapping the model. Within the wrapped module:
- The input (isotropic grid coordinates (X,Y) is normalized.
- The model is inferred.
- The output is un-normalized to get the real output.
So now when inferring through the wrapped model, you pass the a) non-normalized input coordinates, and you get b) non-normalized output velocity distribution. So, when using autograd on the wrapped model to get the derivatives of b) with respect to a), you would expect the gradients to be nearly identical to when using FDM to get the same gradients. But I am seeing a consistent error:
In the centre the error appears to be roughly 30%.
I am fairly confident in my application of the wrapped model. So, is there any interactions in the backwards pass of autograd (maybe layernorms, softmax, accumulated precision overflow etc) that could introduce significant or accumulated errors?
If this is the case, could it be that training would also be affected since this is the primary mechanism of neural networks.
Hmm just to double check, we could use torch.autograd.gradcheck.gradcheck — PyTorch 2.3 documentation to validate the gradients. Underneath it compares the analytical gradient of autograd with that computed by FDM as you are doing.