I have thrown together a dummy model to showcase linear regression in pytorch, but I find that my model is not properly learning. It’s doing well when it comes to learning the slope, but the intercept is not really budging. Printing out the grads at every epoch tells me that, indeed, the grad is a lot smaller for the bias. Why is that? How can I remedy it, so the intercept is properly learnt?
This is what happens (a set to 0 to illustrate):
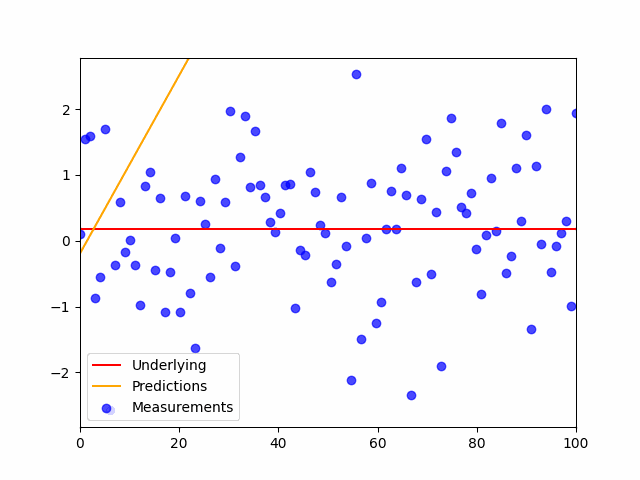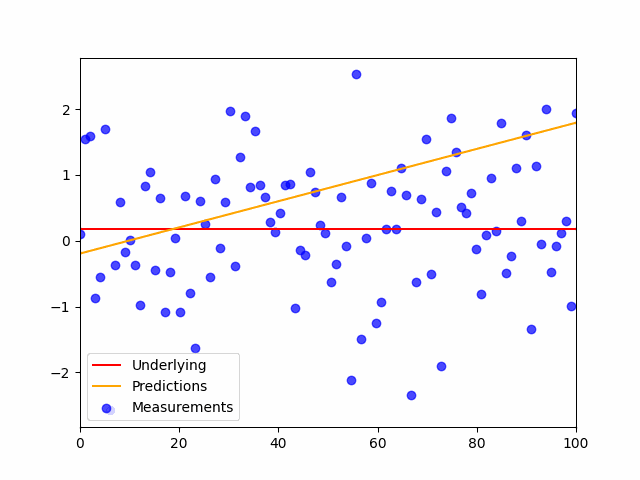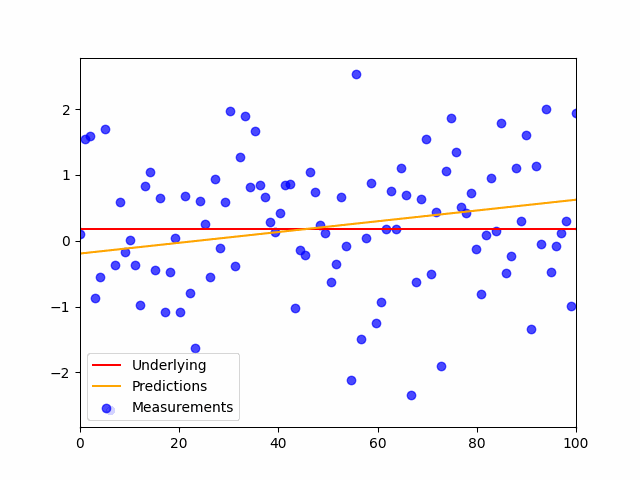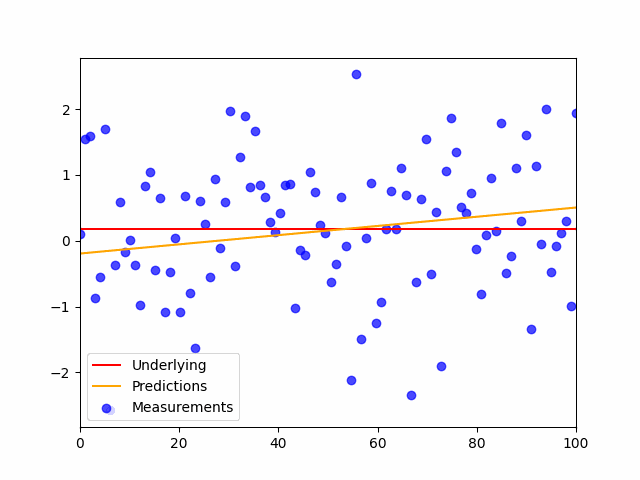
This is the code:
# Create some dummy data: we establish a linear relationship between x and y
a = np.random.rand()
b = np.random.rand()
a=0
x = np.linspace(start=0, stop=100, num=100)
y = a * x + b
# Now let's create some noisy measurements
noise = np.random.normal(size=100)
y_noisy = a * x + b + noise
# What's the overall error?
mse_actual = np.sum(np.power(y-y_noisy,2))/len(y)
# Visualize
plt.scatter(x,y_noisy, label='Measurements', alpha=.7)
plt.plot(x,y,'r', label='Underlying')
plt.legend()
plt.show()
# Let's learn something!
inputs = torch.from_numpy(x).type(torch.FloatTensor).unsqueeze(1)
targets = torch.from_numpy(y_noisy).type(torch.FloatTensor).unsqueeze(1)
# This is our model (one hidden node + bias)
model = torch.nn.Linear(1,1)
optimizer = torch.optim.SGD(model.parameters(),lr=1e-5)
loss_function = torch.nn.MSELoss()
# What does it predict right now?
shuffled_inputs, preds = [], []
for input, target in zip(inputs,targets):
pred = model(input)
shuffled_inputs.append(input.detach().numpy()[0])
preds.append(pred.detach().numpy()[0])
# Visualize
plt.scatter(x,y_noisy, color='blue', label='Measurements', alpha=.7)
plt.plot(shuffled_inputs, preds, color='orange', label='Predictions', alpha=.7)
plt.plot(x,y,'r', label='Underlying')
plt.legend()
plt.show()
# Let's train!
epochs = 100
a_s, b_s = [], []
for epoch in range(epochs):
# Reset optimizer values
optimizer.zero_grad()
# Predict values using current model
preds = model(inputs)
# How far off are we?
loss = loss_function(targets,preds)
# Calculate the gradient
loss.backward()
# Update model
optimizer.step()
# Quick check
for p in model.parameters():
print('Grads:', p.grad)
# New parameters!
a_s.append(list(model.parameters())[0].item())
b_s.append(list(model.parameters())[1].item())
print(f"Epoch {epoch+1} -- loss = {loss}")