Building computational graph

autograd
1

Hello,

I am currently trying to build computational graphs that are then used to build
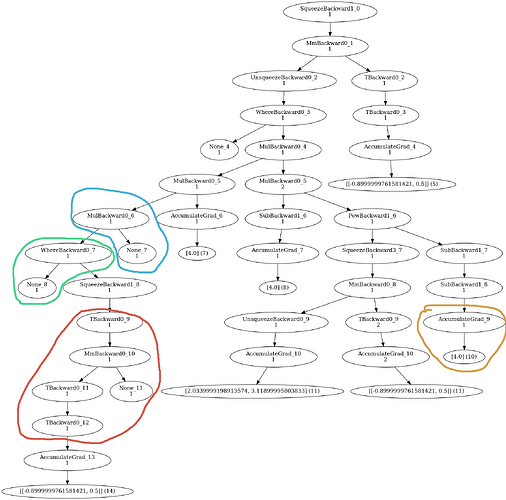
symbolic expressions for SMT solving. However, some things are unclear to me. Below you see a picture of one of my example graphs:

example
example1758×1734 390 KB

(For clarification: The numbers next to “…Backward”, such as _9, only indicate row number in the graph, and numbers below each String indicate duplicates for each row. This is only a detail related to drawing (unique IDs) and is not relevant to my questions)

My questions:

  1. (Red) Why is here a double Transpose?
  2. (Red) What does “None” do here in MmBackward?
  3. (Green) What does “None” do here in WhereBackward?
  4. (Blue) What does “None” do here in MulBackward?

I know that, in the case of PowPackward, if the number to which the base tensor is raised to is not tracked by autograd then that will also appear as “None” in the graph. Now I am wondering what “None” is referring two in the above questions.

Lastly:
5) (Orange) Does AccumulateGrad do something special with [4.0]?

Note: The graph was created as follows:

L = torch.nn.Linear(2, 1, bias=False)
four = torch.tensor([4])
x = torch.tensor([2.034, 3.119])
x.requires_grad = True
four.requires_grad = True #otherwise this would appear as a None node in the graph
with torch.no_grad():
    L.weight[0] = t.tensor([-0.9, 0.5])
y = L(x).pow(four)

#First order derivative
fd = torch.autograd.grad(y, x, create_graph=True)[0]

#Second order derivative
sd = torch.autograd.grad(fd[0], x, create_graph=True)[0]

Now, sd.grad_fn contains the graph depicted above.

Thank you.