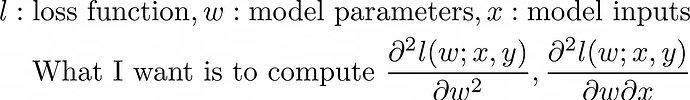Calculating second-order partial derivatives of loss function

1

Hi! I’m trying to calculate: 1) the hessian of the loss function w.r.t. the model parameters 2) first calculate the gradient of loss function w.r.t. the inputs, then differentiate w.r.t the model parameters.
This is my code (first install torchmetrics using pip install torchmetrics):

import torch
from torchmetrics import HingeLoss
import numpy as np

class simple(torch.nn.Module):
    def __init__(self):
        super(simple, self).__init__() 
        self.linear = torch.nn.Linear(in_features=784, out_features=1, bias=True)
    def forward(self, x):
        output = self.linear(x)
        return output

model = simple()

x = torch.Tensor(np.random.rand(5,784)) # 5 dummy data points
y = torch.Tensor([0,1,0,1,0]) # 5 dummy labels

outputs = model(x)
loss_fn = HingeLoss()
loss = loss_fn(outputs, y)

pytorch
pytorch1988×290 26.9 KB

The above-mentioned matrices should be of shape 785x785 and 785x784, respectively.
I’ve searched a lot but none of the previously mentioned questions solved my problem. Is there a neat way to calculate these values?