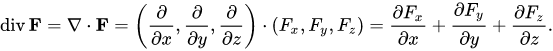How to calculate the divergence efficiently? I’m not talking about a GAN divergence, but the actual divergence which is the sum of the partial derivative of all elements of a vector (Divergence - Wikipedia).
Assume f(x): R^d-> R^d. I could use autograd to get the derivative matrix (of size d x d) and then simply take the sum of the diagonals. But this is seems terribly inefficient and wasteful. There has to be a better way!
Hello Alexia!
The short answer is to use requires_grad = True on
each of your d input variables one at at time, and calculate
one derivative at a time for each of your d output variables.
Then you sum the derivatives together.
But …
I’m not aware of any easy way to do precisely what you want.
The reason is that there is no automatic way to disentangle
calculation that is shared by your d output variables.
In three-dimensional language, if your three output variables
as functions of your three input variables are F_u (x, y, z),
F_v (x, y, z), and F_w (x, y, z), and those three functions
are completely unrelated to one another, then no efficiency is
is lost by calculating them separately, and using three separate
runs of autograd’s backward() to calculate d F_u / d x,
d F_v / d u, and d F_w_ / d z separately.
If F_u, F_v, and F_w have almost all of their calculational
work shared, very little efficiency will be lost by using one run
of autograd’s backward() to calculate all three components
(x, y, and z) of the gradient at the same time and discarding
the off-diagonal elements. That is, you already had to do
almost all of the calculational work needed for the off-diagonal
elements, so the incremental cost of calculating them (and
then not using them) is small.
If F_x, F_y, and F_z have significant shared computation,
but also significant independent computation, you will have to
disentangle the shared computation by hand if you want to
calculate your divergence with maximum efficiency.
If you calculate the three needed partial derivatives independently
(using requires_grad = True one at a time on each variable),
you will be needlessly repeating the shared computation. But if
you calculate the full gradient all at once (performing one
backward() run with requires_grad = True set on all
the input variables at the same time), you will be needlessly
performing the off-diagonal pieces of the “independent”
computation.
Note, in a typical multi-layer neural network, most of the
computation that leads to the value of your output values
will be shared, so, as a practical matter, I would use autograd
to calculate the full gradient all at once, sum the diagonal
elements to get the divergence, and discard the off-diagonal
elements. I would be wasting a little bit of effort to calculate the
off-diagonal elements, but, because most of the calculational
cost was shared in the earlier, upstream layers of the neural
network, the wasted work would likely be small.
Good luck.
K. Frank
Thanks @KFrank , I appreciate the well thought response. I will try both approaches.
Hi @AlexiaJM!
Did you figure out a way to do perform this computation efficiently?
Hope I’m not late. I think there are two ways, 1) Divergence = Trace(Jacobian). This is a trivial extension of the definition, however, computation of Jacobian using torch.autograd.functional.jacobian might be memory intensive. 2) You can use the torch.autograd.grad module for this.
Example,
from torch.autograd import grad
# Assuming your_inp is of size (B,N,3)
g = grad(your_network_callable, your_inp, grad_outputs=torch.ones_like(your_inp), create_graph=True)[0]
@ptrblck can you please confirm if my soln is correct? Thank you!
Maybe this will help you :