Cannot learn through single FFT call

1

Hello,

while playing around with a model that will feature calls to the fft functions, I have noticed something odd about the behavior of the gradient. Basically, I cannot do a basic gradient descent when I have exact target data. My starting point is some volumetric data in the shape [1, size, size, size], so three dimensional, with an additional dimension for batch size.
Now if I start with a zeroed volume, then do a rfftn call and then calculate an error based on the FFT of my target volume, I end up with no learning whatsoever. Here is my sample code:

import torch
import torch.fft
import torch.optim

import numpy as np

cuda0 = torch.device('cuda:0')

size = 178

#Target volume
tensorImage = torch.zeros([1, size, size, size], dtype=torch.float32)
for x in range(178):
   # Circle
   if pow(x - size/2,2) > 10:
       continue
   for y in range(178):
       if pow(y - size/2,2) > 10:
           continue
       for z in range(178):
           if pow(z - size/2,2) > 10:
               continue
           tensorImage[0,z,y,x] = 1

           
tensorImage = tensorImage.to(cuda0)
tensorFFT = torch.fft.rfftn(tensorImage, dim=(1,2,3))

#Starting volume, with only 0s
tensorZeroImage = torch.zeros(tensorImage.size(), requires_grad=True, device=cuda0)
optim = torch.optim.SGD([tensorZeroImage], lr=0.01)

for i in range(1000):
   optim.zero_grad()                     
   tensorFFTZero = torch.fft.rfftn(tensorZeroImage, dim=(1,2,3))
   tensorFFTDiff = tensorFFTZero - tensorFFT
   tensorFFTDiffAbs = tensorFFTDiff.abs()
   tensorFFTDiffAbsSqrd = tensorFFTDiffAbs
   error = tensorFFTDiffAbsSqrd.sum()

   error.backward()
   optim.step()
   if (i+1)%100==0:
       print(error)

Output is

tensor(8.2181e+10, device='cuda:0', grad_fn=<SumBackward0>)
tensor(8.2181e+10, device='cuda:0', grad_fn=<SumBackward0>)
tensor(8.2181e+10, device='cuda:0', grad_fn=<SumBackward0>)
tensor(8.2181e+10, device='cuda:0', grad_fn=<SumBackward0>)
tensor(8.2181e+10, device='cuda:0', grad_fn=<SumBackward0>)
tensor(8.2181e+10, device='cuda:0', grad_fn=<SumBackward0>)
tensor(8.2181e+10, device='cuda:0', grad_fn=<SumBackward0>)
tensor(8.2181e+10, device='cuda:0', grad_fn=<SumBackward0>)
tensor(8.2181e+10, device='cuda:0', grad_fn=<SumBackward0>)
tensor(8.2181e+10, device='cuda:0', grad_fn=<SumBackward0>)

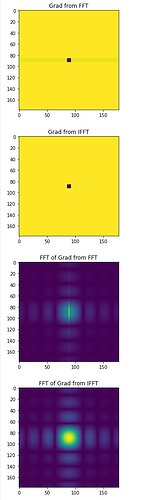
So no learning whatsoever. There seems to be something odd about the backpropagation through the rfftn call (or fftn).

If I add an ifftn call and then compare the two volumes directly, I get correct learning as expected.

Is there any explanation, why the code above with an error calculation on the fourier transform does not work as expected?

2

I don’t think the backpropagation is wrong, but your loss is just extremely high, which would also create large gradients and could thus break the training.
If you use a mean() as the error, you’ll see that (some) training is happening:

tensor(5.0114, device='cuda:0', grad_fn=<MeanBackward0>)
tensor(4.5654, device='cuda:0', grad_fn=<MeanBackward0>)
tensor(4.2215, device='cuda:0', grad_fn=<MeanBackward0>)
tensor(3.9387, device='cuda:0', grad_fn=<MeanBackward0>)
tensor(3.7002, device='cuda:0', grad_fn=<MeanBackward0>)
tensor(3.4965, device='cuda:0', grad_fn=<MeanBackward0>)
tensor(3.3204, device='cuda:0', grad_fn=<MeanBackward0>)
tensor(3.1662, device='cuda:0', grad_fn=<MeanBackward0>)
tensor(3.0293, device='cuda:0', grad_fn=<MeanBackward0>)
tensor(2.9056, device='cuda:0', grad_fn=<MeanBackward0>)
3

Hi @ptrblck
thank you for your quick reply. You are correct with the loss and therefore gradient being too large for any good training. With enough iterations, it actually recovers the original image. There is still something odd I am noticing about the exact gradient in the first iteration. I have an extended sample code below:

import torch
import torch.fft
import torch.optim

import numpy as np

cuda0 = torch.device('cuda:0')

size = 178

#Target volume
tensorImage = torch.zeros([1, size, size, size], dtype=torch.float32)
for x in range(178):
    # Circle
    if pow(x - size/2,2) > 10:
        continue
    for y in range(178):
        if pow(y - size/2,2) > 10:
            continue
        for z in range(178):
            if pow(z - size/2,2) > 10:
                continue
            tensorImage[0,z,y,x] = 1

            
tensorImage = tensorImage.to(cuda0)
tensorFFT = torch.fft.rfftn(tensorImage, dim=(1,2,3))

#Starting volume, with only 0s
tensorZeroImage = torch.zeros(tensorImage.size(), requires_grad=True, device=cuda0)
               
tensorFFTZero = torch.fft.rfftn(tensorZeroImage, dim=(1,2,3))
tensorFFTDiff = tensorFFTZero - tensorFFT
tensorFFTDiffAbs = tensorFFTDiff.abs()
tensorFFTDiffAbsSqrd = tensorFFTDiffAbs.pow(2)
error = tensorFFTDiffAbsSqrd.mean()

error.backward()
gradientFromFFT = tensorZeroImage.grad
np_gradientFromFFT = gradientFromFFT.cpu().detach().numpy()

tensorZeroImage = torch.zeros(tensorImage.size(), requires_grad=True, device=cuda0)
               
tensorFFTZero = torch.fft.rfftn(tensorZeroImage, dim=(1,2,3))
tensorIFFTZero = torch.fft.irfftn(tensorFFTZero, dim=(1,2,3))
tensorIFFTDiff = tensorIFFTZero - tensorImage
tensorIFFTDiffSqrd = tensorIFFTDiff.pow(2)
error = tensorIFFTDiffSqrd.mean()

error.backward()
gradientFromIFFT = tensorZeroImage.grad
np_gradientFromIFFT = gradientFromIFFT.cpu().detach().numpy()

import matplotlib.pyplot as plt
plt.figure()
plt.imshow(np_gradientFromFFT[0,89,:,:])
plt.figure()
plt.imshow(np_gradientFromIFFT[0,89,:,:])
plt.show()

This is the result:

2021-06-28 10_17_58-Untitled - Jupyter Notebook
2021-06-28 10_17_58-Untitled - Jupyter Notebook325×1094 46.3 KB

There is an odd looking artifact when calculating the loss based on the difference in fourier space compared to adding an additional irfftn call.