Hi all,
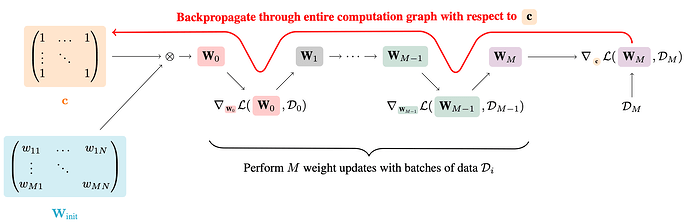
I’m trying to keep this post somewhat short but I’m happy to provide additional details if necessary. I’m trying to implement ProsPr pruning as proposed by Alizadeh et al. (2022). The basic idea is to add a masking c (i.e. matrix of all ones) to all to-be-pruned layers at initialization and then perform M batches of training (5 at most), as visualized by figure 1 in the paper:
After the M iterations, the derivative for each mask element is computed, which requires using the chain rule, as illustrated by equation 6-10 in the original paper:
The original implementation achieves this via monkey-patching and re-implementing SGD with a lot of additional storage overhead. I would like to avoid that, if possible.
My idea is to add the weight masks as parameters and set their learning rates to 0, since the masks need to stay constant but also need to have a gradient per step (see equation (10)). I achieves this by initializing the optimizer as follows:
weights = [
param for name, param in model.named_parameters() if name.endswith(".weight")
]
weight_masks = [
param for name, param in model.named_parameters() if name.endswith(".weight_mask")
]
# Initialize optimizer
inner_sgd: SGD = SGD(
[{"params": weights}, {"params": weight_masks, "lr": 0.0}],
lr=learning_rate,
momentum=learning_momentum,
)
During training, I then use autograd to be able to create/retain the computation graph:
grads = torch.autograd.grad(
outputs=loss,
inputs=self.model.parameters(),
create_graph=True,
retain_graph=True
)
I then clone each gradient to the respective layer using a for loop and grads[i].clone(), since autograd does not apply the gradients (unlike optimizer.step()).
From what I’ve read on the computation graph, this should allow me to implement the chain rules as given by equation (6) by simply applying autograd after the training has finished:
torch.autograd.grad(loss, weight_masks, create_graph=False, retain_graph=True)
However, since I do not understand the inner workings of the graph completely (yet), I am not sure whether my assumptions and implementation are correct. As reference: My results diverge slightly from the original implementation, but the differences in computed thresholds are small enough that one might consider them to be related to numerical differences.
I would appreciate any input on whether this actually makes sense or whether I did something wrong. Thanks in advance!