Hello there,
I am trying to implement the ciruclar correlation defined as follows:
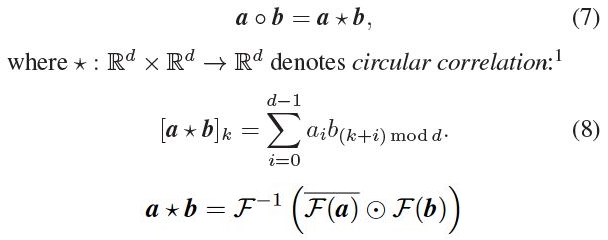
which can be efficiently calculated using the Fourier transformation (and its inverse), the elementwise product and the complex negation.
I am new to PyTorch and don’t know whether, this is possible and if so, whether it was already implemented.
I tried it like this:
complex_s = complex_conjugation(torch.rfft(s, 1, onesided=False))
complex_o = torch.rfft(o, 1, onesided=False)
circular_correlation = torch.irfft(elementwise_complex_multiplication(complex_s, complex_o), 1, onesided=False)
def complex_conjugation(tensor):
minor = tensor.clone()
for i in range(minor.size(-1)):
minor[i, 0] = 0
res = tensor - 2 * minor
return res
def real_part(tensor):
dimensions = len(list(tensor.size()))
return tensor.narrow(dimensions-1, 0, 1)
def imag_part(tensor):
dimensions = len(list(tensor.size()))
return tensor.narrow(dimensions-1, 1, 1)
def elementwise_complex_multiplication(t1, t2):
dimensions1 = len(list(t1.size()))
dimensions2 = len(list(t2.size()))
if dimensions1 != dimensions2:
print("Different number of tensor dimensions in elementwise_complex_multiplication")
exit(1)
real1 = real_part(t1)
real2 = real_part(t2)
imag1 = imag_part(t1)
imag2 = imag_part(t2)
return torch.cat((real1 * real2 - imag1 * imag2, real1 * imag2 + imag1 * real2), dim=dimensions1-1)
However, I don’t get the same results, as when I use the formula of the definition (without fft).
I tested my self-defined functions and they should be correct.
I don’t know, whether I understood torch.rfft and torch.irfft correctly.
Please don’t be too harsh with me. Thank you already for looking into this.
PS: I compute it as part of the forward method in a network. Is this autograd compatible and is there maybe another way to implement it more efficiently?
Best regards
Chrixtar