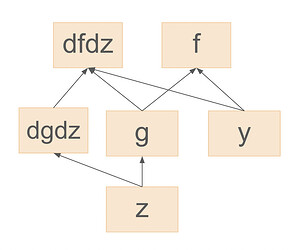
Hello all,
I have the following issue:
I have a function that takes as input a pretrained model (eg. GAN) and another vector y, let’s say
f(y, G(z)) .
I want to compute the gradient of this function w.r.t. to z_i for different (and many) z_i’s. Let us denote this gradient as:
dfdz = []
for i in range(N):
dfdz.append(autorgrad.grad(f(y,G(z_i)),z_i, create_graph= True)[0])
That gradient is a function of y and the jacobian of G(z_i). Then, all the gradients dfdz = [dfdz[1] dfdz[2],…,dfdz[N] ] are given as input to another function g(dfdz,x) and I want to get the gradient of g(dfdz,x) w.r.t. y (let’s denote it as dgdy).
The issue is that when I use create_graph = True, which is needed for being able the gradient of g(dfdz,x), the CUDA memory blows up. I have checked the computation graph and it seems that for each z_i Pytorch saves in memory the computation graph of G(z_i) which is huge.
However, I don’t need the compuation graph for G(z_i) which is a pretrained model. In fact, I only care about its gradients w.r.t. to z (Jacobians).
Is there any way to delete from memory that part of the graph ?
If not, is there any alternative and efficient way to perform the same computations without setting create_graph to True?
Thank you !