Hello, I have an issue related to computing the Jacobian matrix of a model. I’ve trained a model on a 4-input 4-output equation set, which performs well in fitting the original equations. My goal is to derive the Jacobian matrix of partial derivatives from the model’s output layer to its input layer, utilizing torch.autograd.functional.jacobian() to obtain both the model’s and equation set’s Jacobian matrices. However, the results significantly differ between the two, and this discrepancy persists even after experimenting with different network architectures (fast-KAN, efficient-KAN, MLP). I speculate that the issue might lie in the de-normalization process of the Jacobian matrix. How can I improve this?
My primary approach is as follows:
- Normalize the training input and output data (e.g.,
x_out = (x - x_min) / range_of_x) to fall within [0,1]. - Fit normalized data into the model, then de-normalize outputs to assess fitting quality.
- Employ
torch.autograd.functional.jacobian()to get the Jacobians; normalize model inputs but use raw data for the equation set. - De-normalize the model’s Jacobian matrix by multiplying each row by the range of the respective output variable (
range of F_n), and dividing each column by the range of the corresponding input variable (range of x_n).
The code snippet for training the model is as follows:
import torch.nn as nn
# from efficient_kan import KAN
from fastkan import FastKAN as KAN
from torch import optim
from tqdm import tqdm
from sklearn.metrics import r2_score
from normalize_data import *
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
train_loader, val_loader = load_data('olhs_samples.csv', 4, 0.3, 16)
# Define model structure
model = KAN([4, 30, 30, 4]) # Input 4 values, first hidden layer is 30 neurons, second hidden layer is 30 neurons, output 4 values
# model = nn.Sequential(
# nn.Linear(4, 100),
# nn.Sigmoid(),
# nn.Linear(100, 100),
# nn.Sigmoid(),
# nn.Linear(100, 100),
# nn.Sigmoid(),
# nn.Linear(100, 100),
# nn.Sigmoid(),
# nn.Linear(100, 4)
# )
model.to(device)
optimizer = torch.optim.AdamW(model.parameters(), lr=1e-3, weight_decay=1e-4)
scheduler = torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.8)
criterion = nn.MSELoss() # Use Mean Square Error as Loss Function
# train
num_epochs = 30
for epoch in range(num_epochs):
model.train()
running_loss = 0.0
for inputs, targets in tqdm(train_loader):
inputs, targets = inputs.to(device), targets.to(device)
optimizer.zero_grad()
outputs = model(inputs.to(device))
loss = criterion(outputs, targets.to(device))
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item()*inputs.size(0)
# verification model
model.eval()
val_loss = 0.0
all_preds = []
all_targets = []
with torch.no_grad():
for inputs, targets in val_loader:
inputs, targets = inputs.to(device), targets.to(device)
outputs = model(inputs)
val_loss += criterion(outputs, targets.to(device)).item()*inputs.size(0)
all_preds.append(outputs.cpu().numpy())
all_targets.append(targets.cpu().numpy())
# Calculate average loss and R² score
avg_val_loss = val_loss / len(val_loader)
avg_train_loss = running_loss / len(train_loader)
all_preds = np.concatenate(all_preds)
all_targets = np.concatenate(all_targets)
r2 = r2_score(all_targets, all_preds)
print(f"Epoch {epoch + 1}/{num_epochs}, Train Loss: {avg_train_loss:.10f}, Val Loss: {avg_val_loss:.10f}, R² Score: {r2:.10f}")
# update learning rate
scheduler.step()
# Save model after training
torch.save(model.state_dict(), 'trained_model.pth')
print("Model saved successfully.")
Data fitting and Jacobi matrix calculation:
# from efficient_kan import KAN
from fastkan import FastKAN as KAN
from torch.autograd.functional import jacobian
from normalize_data import *
import torch.nn as nn
from sklearn.metrics import r2_score
# Load trained models
# model = KAN(layers_hidden=[4, 100, 100, 100, 4], grid_size=5, spline_order=3)
model = KAN(layers_hidden=[4, 30, 30, 4])
# model = nn.Sequential(
# nn.Linear(4, 100),
# nn.Sigmoid(),
# nn.Linear(100, 100),
# nn.Sigmoid(),
# nn.Linear(100, 100),
# nn.Sigmoid(),
# nn.Linear(100, 100),
# nn.Sigmoid(),
# nn.Linear(100, 4)
# )
model.load_state_dict(torch.load('trained_model.pth'))
model.eval()
# reads the input data
raw_input_dataframe = pd.read_csv('olhs_input.csv')
input_data = normalize_data(raw_input_dataframe, 'olhs_samples_max_min.csv', False).values.astype(np.float32)
raw_input_data = raw_input_dataframe.values.astype(np.float32)
# Converting data to PyTorch tensors
raw_inputs = torch.tensor(raw_input_data, dtype=torch.float32, requires_grad=True)
inputs = torch.tensor(input_data, dtype=torch.float32, requires_grad=True)
# Using models for forecasting
raw_predictions = model(inputs).detach().numpy()
x_num = 4 # Number of input variables
f_num = 4 # Number of output variables
raw_predictions = pd.DataFrame(raw_predictions, columns=[f'f{i+1}' for i in range(f_num)])
# Calculate true output
true_outputs = np.array([fn_4i4o(*row) for row in raw_input_data])
# inverse normalization
predictions = normalize_data(raw_predictions, 'olhs_samples_max_min.csv', True)
# Read maximum and minimum values from CSV file
max_min_data = pd.read_csv('olhs_samples_max_min.csv')
# Calculate the domain interval length and range interval length for each variable
range_ranges = max_min_data['Max'][:x_num] - max_min_data['Min'][:x_num]
domain_ranges= max_min_data['Max'][x_num:] - max_min_data['Min'][x_num:]
# Assign input data to result DataFrame
results_df = raw_input_dataframe.copy()
def true_forward(input_tensor):
"""
Compute the output of the equations
"""
x1, x2, x3, x4 = input_tensor[0], input_tensor[1], input_tensor[2], input_tensor[3]
f1 = 0.4 * x1 ** 2 + 0.2 * x2 ** 2 + 0.1 * x3 ** (7 / 2) + 0.3 * x4 ** (3 / 2)
f2 = 3 * x1 + 4 * x2 + 5 * x3 + 6 * x4 + torch.sin(x1) * torch.cos(x2)
f3 = torch.sin(x1) + torch.cos(x2) + 0.05 * torch.exp(x3) + 0.1 * torch.exp(x4)
f4 = 200 * x1 ** 2 + 6 * torch.exp(x2) + 1 * x1 ** 3 + 4 * torch.exp(x4)
output_tensor = torch.stack([f1, f2, f3, f4])
return output_tensor
# Defines a function that accepts the input tensor and returns the output tensor of the model
def model_forward(x):
return model(x)
# Calculates the partial derivative (first derivative) of the model output with respect to the input
for i in range(inputs.shape[0]):
jacobians_true = jacobian(true_forward, raw_inputs[i])
jacobians = jacobian(model_forward, inputs[i])
# The calculated partial derivatives are normalized.
denormalized_jacobians = torch.zeros_like(jacobians)
for m in range(jacobians.shape[0]):
for n in range(jacobians.shape[1]):
denormalized_jacobians[m, n] = jacobians[m, n] / range_ranges[n] * domain_ranges[m + x_num]
# Convert PyTorch Tensors to NumPy Arrays
model_derivatives_np = denormalized_jacobians.detach().numpy()
exact_derivatives_np = jacobians_true.detach().numpy()
# Dynamically generate column names and add them to DataFrame
for j in range(jacobians.shape[0]):
for k in range(jacobians.shape[1]):
results_df.loc[i, f'df{j + 1}_dx{k + 1}'] = model_derivatives_np[j, k]
results_df.loc[i, f'df{j + 1}_dx{k + 1}_true'] = exact_derivatives_np[j, k]
# Save jacobian_results to CSV file
results_df.to_csv('jacobian_results.csv', index=False)
# Save results to CSV
results = {
'x1': raw_input_data[:, 0],
'x2': raw_input_data[:, 1],
'x3': raw_input_data[:, 2],
'x4': raw_input_data[:, 3],
'Predicted_f1': predictions['f1'].values,
'Predicted_f2': predictions['f2'].values,
'Predicted_f3': predictions['f3'].values,
'Predicted_f4': predictions['f4'].values,
'True_f1': true_outputs[:, 0],
'True_f2': true_outputs[:, 1],
'True_f3': true_outputs[:, 2],
'True_f4': true_outputs[:, 3],
}
# Convert to DataFrame and save
df_results = pd.DataFrame(results)
df_results.to_csv('prediction.csv', index=False)
Neural network structure in FastKAN:
class SplineLinear(nn.Linear):
def __init__(self, in_features: int, out_features: int, init_scale: float = 0.1, **kw) -> None:
self.init_scale = init_scale
super().__init__(in_features, out_features, bias=False, **kw)
def reset_parameters(self) -> None:
nn.init.trunc_normal_(self.weight, mean=0, std=self.init_scale)
class RadialBasisFunction(nn.Module):
def __init__(
self,
grid_min: float = -2.,
grid_max: float = 2.,
num_grids: int = 8,
denominator: float = None, # larger denominators lead to smoother basis
):
super().__init__()
grid = torch.linspace(grid_min, grid_max, num_grids)
self.grid = torch.nn.Parameter(grid, requires_grad=False)
self.denominator = denominator or (grid_max - grid_min) / (num_grids - 1)
def forward(self, x):
return torch.exp(-((x[..., None] - self.grid) / self.denominator) ** 2)
class FastKANLayer(nn.Module):
def __init__(
self,
input_dim: int,
output_dim: int,
grid_min: float = -2.,
grid_max: float = 2.,
num_grids: int = 8,
use_base_update: bool = True,
base_activation = F.silu,
spline_weight_init_scale: float = 0.1,
) -> None:
super().__init__()
self.layernorm = nn.LayerNorm(input_dim)
self.rbf = RadialBasisFunction(grid_min, grid_max, num_grids)
self.spline_linear = SplineLinear(input_dim * num_grids, output_dim, spline_weight_init_scale)
self.use_base_update = use_base_update
if use_base_update:
self.base_activation = base_activation
self.base_linear = nn.Linear(input_dim, output_dim)
def forward(self, x, time_benchmark=False):
if not time_benchmark:
spline_basis = self.rbf(self.layernorm(x))
else:
spline_basis = self.rbf(x)
ret = self.spline_linear(spline_basis.view(*spline_basis.shape[:-2], -1))
if self.use_base_update:
base = self.base_linear(self.base_activation(x))
ret = ret + base
return ret
class FastKAN(nn.Module):
def __init__(
self,
layers_hidden: List[int],
grid_min: float = -2.,
grid_max: float = 2.,
num_grids: int = 8,
use_base_update: bool = True,
base_activation = F.silu,
spline_weight_init_scale: float = 0.1,
) -> None:
super().__init__()
self.layers = nn.ModuleList([
FastKANLayer(
in_dim, out_dim,
grid_min=grid_min,
grid_max=grid_max,
num_grids=num_grids,
use_base_update=use_base_update,
base_activation=base_activation,
spline_weight_init_scale=spline_weight_init_scale,
) for in_dim, out_dim in zip(layers_hidden[:-1], layers_hidden[1:])
])
def forward(self, x):
for layer in self.layers:
x = layer(x)
return x
Here are the parameters of one of the layers of the model I trained using FastKAN with five neurons in a hidden layer:
‘layers.0.layernorm.weight’, 1x4matrix
‘layers.0.layernorm.bias’, 1x4matrix
‘layers.0.rbf.grid’, 1x8matrix
‘layers.0.spline_linear.weight’, 8x5matrix
‘layers.0.base_linear.weight’, 5x4matrix
‘layers.0.base_linear.bias’, 1x5matrix
There are other functions and code that I’ll give you if you need them.
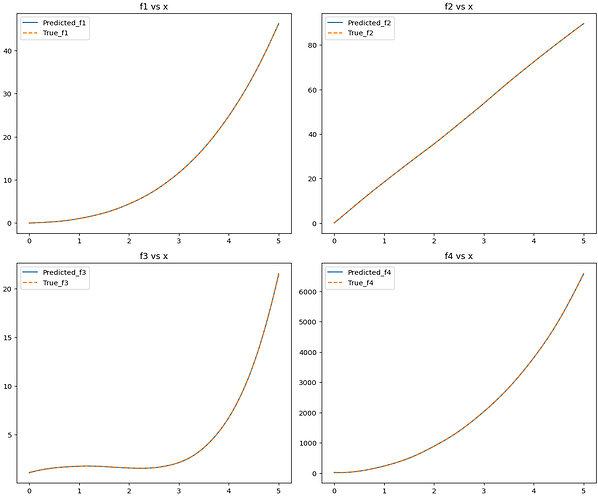
Data fit:
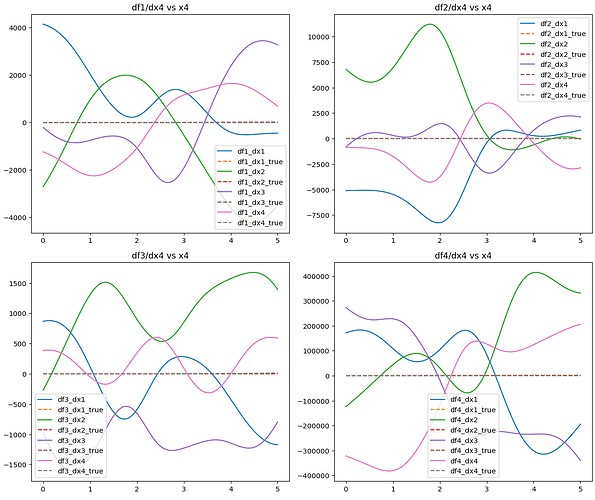
Jacobian(FastKAN,Different neural networks have different results.)