Compute mse_loss() with softmax()

Mukesh1729 · November 22, 2021, 8:33am

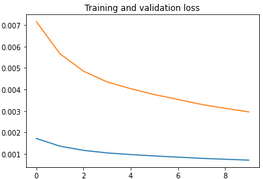
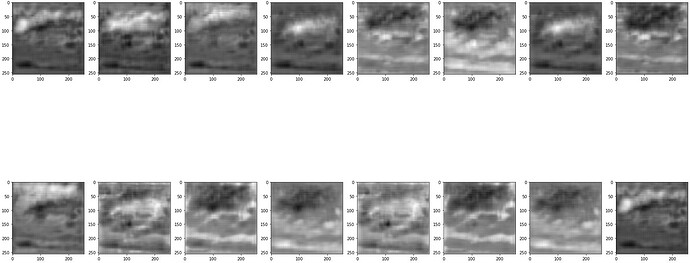
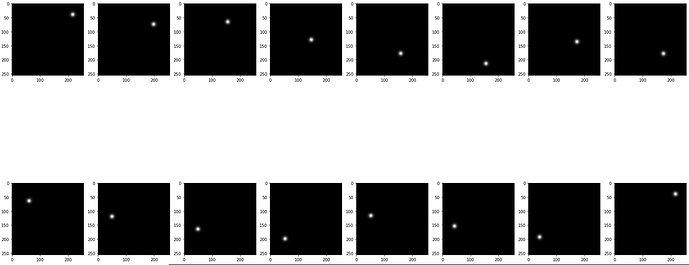
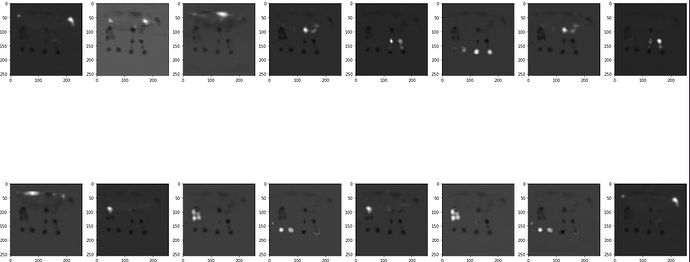
Hi I am using using a network that produces an output heatmap (torch.rand(1,16,1,256,256)) with
Softmax( ) as the last network activation.
I want to compute the MSE loss between the output heatmap and a target heatmap.
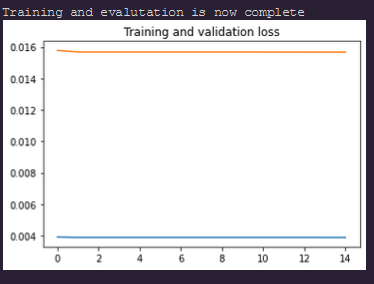
When I add the softmax the network loss doesn’t decrease and is around the same point and works when I remove the softmax.

How can I go about computing mse loss by using softmax()?
Thanks

from torch.nn import init
class NET(torch.nn.Module):
    def __init__(self):
        super(NET, self).__init__()
        self.encoder = torch.nn.Sequential(
                                          torch.nn.Conv3d(3, 64, kernel_size=(3,3,3), stride=(1,1,1), padding=(1,1,1)),
                                          torch.nn.BatchNorm3d(num_features=64),
                                          torch.nn.ReLU(inplace=True),
                                          torch.nn.MaxPool3d(kernel_size=(1,2,2),stride=(1,2,2)),
            
                                          torch.nn.Conv3d(64, 128, kernel_size=(3,3,3), stride=(1,1,1), padding=(1,1,1)),                                         
                                          torch.nn.BatchNorm3d(num_features=128),
                                          torch.nn.ReLU(inplace=True),
                                          torch.nn.MaxPool3d(kernel_size=(2,2,2),stride=(2,2,2)),
                                          
                                           
                                          torch.nn.Conv3d(128, 256, kernel_size=(3,3,3), stride=(1,1,1), padding=(1,1,1)),
                                          torch.nn.BatchNorm3d(num_features=256),
                                          torch.nn.ReLU(inplace=True),
                                          torch.nn.MaxPool3d(kernel_size=(1,2,2),stride=(1,2,2)),
                                         
                                           
                                          torch.nn.Conv3d(256, 512, kernel_size=(1,3,3), stride=(1,1,1), padding=(1,1,1)),
                                          torch.nn.BatchNorm3d(num_features=512),
                                          torch.nn.ReLU(inplace=True),
                                          
                                          
                                          )
        
        self.decoder = torch.nn.Sequential(
                                          torch.nn.ConvTranspose3d(512, 256, kernel_size=(1,3,3), stride = (1,2,2), padding=(1,1,1), output_padding=(0,1,1)),
                                          torch.nn.BatchNorm3d(num_features=256), 
                                          torch.nn.ReLU(inplace=True),
                                           
                                                                                  
                                          torch.nn.Conv3d(256, 256, kernel_size=(1,3,3), stride=(1,1,1), padding=(1,1,1)),
                                          torch.nn.BatchNorm3d(num_features=256),
                                          torch.nn.ReLU(inplace=True),
                                          
                                          
                                           
                                          torch.nn.ConvTranspose3d(256,128, kernel_size=(1,3,3), stride = (1,2,2), padding=(1,1,1),output_padding=(0,1,1)), 
                                          torch.nn.BatchNorm3d(num_features=128),
                                          torch.nn.ReLU(inplace=True),
                                          
                                           
                                          torch.nn.Conv3d(128, 128, kernel_size=(1,3,3), stride=(1,1,1), padding=(1,1,1)),
                                          torch.nn.BatchNorm3d(num_features=128),
                                          torch.nn.ReLU(inplace=True),
                                          

                                          torch.nn.ConvTranspose3d(128,16, kernel_size=(1,3,3), stride = (1,2,2), padding=(1,1,1),output_padding=(0,1,1)),
                                          )                  

    def forward(self, image):
        
        encoder = self.encoder(image)
        decoder = self.decoder(encoder)
        return torch.nn.Softmax(dim=1)(decoder)

KFrank · November 22, 2021, 1:39pm

Hi Mukesh!

As a practical matter, I would suggest not using softmax() for the
simple reason that your network trains better without it than with it.

Most of what we know about what works with neural networks comes
not from theory or mathematical proofs, but from experience. So go
ahead and do what your experience with your use case shows works.

I can give some hand-waving intuition about why softmax() might
not be a good fit with mse_loss(). The “mse” in mse_loss() stands
for “mean-squared-error.” Roughly speaking, this is the variance of
the mismatch between your predictions and targets (and the variance
is the square of the standard deviation). Standard deviations and
variances “naturally” work in a context where the values involved are
unconstrained and run from -inf to inf. Your softmax() takes
such unbounded values and forces them to be probability-like values
that range over [0.0, 1.0].

This doesn’t mean that using softmax() couldn’t work or be a good
choice for your use case, but this intuition suggests that softmax()
isn’t a natural fit when using mse_loss().

Best.

K. Frank.

Mukesh1729 · November 22, 2021, 1:55pm

Hey Frank, thanks for the tip. I am trying to replicate a paper and they state:

The last convolutional layer of the decoder is followed by a
transposed-convolutional layer that uses a linear activation followed by a Softmax transformation, resulting in an output
of 17 confidence maps, one per keypoint.
ref : [2104.08029] T-LEAP: occlusion-robust pose estimation of walking cows using temporal information
When i use softmax as the last layer as suggested in the model then my loss stagnates. It would be nice to know how I can use the softmax (before or after, how should my target heatmap look like then) with the mse loss. An example would be helpful

For now, i am doing something like this:

input = model + torch.nn.Softmax(dim=1) (torch.rand(1,16,2,256,256))
heatmap = torch.rand(1,16,1,256,256)
criterion = torch.nn.MSELoss()
criterion(input, heatmap)

KFrank · November 22, 2021, 6:32pm

Hi Mukesh!

I’m not familiar with your use case and I haven’t looked at the paper
you cite, so what I say will be speculation. Nonetheless:

The term “confidence map” (together with the use of Softmax)
suggests to me that you might be dealing with probability-like
values. If so, cross-entropy (or some other probability-comparison
metric such as the Kullback-Leibler divergence) might be more
appropriate.

Your discussion suggests that your target heatmap is not made up
of categorical labels, but rather, of continuous probability-like values.

Pytorch’s built-in CrossEntropyLoss does not support such “soft”
labels, although they do make perfect sense. If you want to explore
the cross-entropy approach, you will have to write your own “soft-label”
version of cross entropy, which is easy enough to do as described here:

Note, when doing this you still do not want a final Softmax layer.
The input to softXEnt() will be the output of your final Linear
layer, understood to be raw-score logits. The target to softXEnt()
will, however, be probability-like values that range over [0.0, 1.0].

I do have some questions about the shapes of your input and
heatmap.

First, what do the dimensions mean?

Second, you mention “17 confidence maps” while the second
dimension of your shapes is 16. Should those values be the same,
or is 16 an unrelated value with a different meaning?

Last, regardless of the meanings of the dimensions, your input and
heatmap have different shapes, which is logically inappropriate for
MSELoss. (MSELoss will broadcast, but you probably don’t want
that.) Why is the third dimension of input 2, and is that really what
you want?

Best.

K. Frank

Mukesh1729 · November 23, 2021, 9:00am

Hey Frank,

The term “confidence map” (together with the use of Softmax)
suggests to me that you might be dealing with probability-like
values - Yes, I am want the probability of a finding a keypoint in a heatmap
I mention 16 confidence maps instead of 17 because I am using 16 keypoints - 1 per channel
Regarding the input output shape of images they look like below:
Input shape = torch.rand(1,16,2,256,256) # 2 refers to the depth (in my case images)
model output = torch.rand(1,16,1,256,256)
target shape = torch.rand(1,16,1,256,256)

Considering the last layer of my model is not a softmax layer but a convtranspose layer with no subsequent activation. Does the implementation look right? The values looks large

def softXEnt (input, target):
    logprobs = torch.nn.functional.log_softmax (input, dim = 1)
    return  -(target * logprobs).sum() / input.shape[0]

input  = torch.rand(1, 16, 1, 256, 256)
target = torch.rand(1, 16, 1, 256, 256)
softXEnt(input, target)

output:tensor(1474121.)

KFrank · November 23, 2021, 4:19pm

Hi Mukesh!

Three comments:

First, if this really is the shape of the “image” you pass into your NET
model, it won’t work. From your first post, the initial layer of NET is:

torch.nn.Conv3d(3, 64, kernel_size=(3,3,3), stride=(1,1,1), padding=(1,1,1))

That is, your Conv3d layer expects in_channels = 3, and you are
passing in a tensor with in_channels (the second dimension) equal
to 16.

def softXEnt (input, target):
    logprobs = torch.nn.functional.log_softmax (input, dim = 1)
    return  -(target * logprobs).sum() / input.shape[0]

input  = torch.rand(1, 16, 1, 256, 256)
target = torch.rand(1, 16, 1, 256, 256)
softXEnt(input, target)

output:tensor(1474121.)

Second, as written, the softXEnt() code I posted is taking the mean
over the batch (in your example, batch-size = 1), but is taking the sum
over the image dimensions (in your case, 1x256x256).

(The softXEnt() code I wrote wasn’t directed at the “multidimensional
case” with trailing “image” dimensions.)

If you prefer to average the loss over the image dimensions (which
might be more natural), you could do something like:

def softXEnt (input, target):
    logprobs = torch.nn.functional.log_softmax (input, dim = 1)
    return  -(target * logprobs).mean()

(I don’t know why I didn’t just use .mean() in the first place.)

Third, you are using input = torch.rand(1, 16, 1, 256, 256).
I realize that this is just an example, but this input consists of values
that range over [0.0, 1.0] (because you are using rand()). Such
values look like probabilities. Make sure that your actual input to
softXEnt() (or CrossEntropyLoss, for that matter) consists of logits
that run from -inf to inf, and not probabilities. (If you wanted to make
your example more realistic in this regard, you could use randn() in
place of rand().)

Best.

K. Frank

Mukesh1729 · November 23, 2021, 5:06pm

Hey Frank,

Thanks for getting back. Regarding the dimensions of the image that was a typo, but I have tried what you suggested and it works:

def softXEnt (input, target):
    logprobs = torch.nn.functional.log_softmax (input, dim = 1)
    return  -(target * logprobs).mean()

# Input image to the model: (1, 3, 2 ,256, 256) 

#Ouput from the model                  
model_out  = torch.randn(1, 16, 1 ,256, 256)
#Target heatmap
target_hmp = torch.randn(1, 16, 1 ,256, 256)

softXEnt(model_out, target_hmp)

output:tensor(-0.0006)

I added the above loss to my training loop and the loss looks like this. It starts off very low
I am using around 400 training images and 100 validation images
Legends:
blue: training
yellow:validation

Training loop

def loss_plot(epochs, train, val):
    ep = [i for i in range(epochs)]
    plt.plot(ep,train,label="Training loss")
    plt.plot(ep,val,label="Validation loss")
    plt.title("Training and validation loss")
    plt.show()
    
def softXEnt (input, target):
    logprobs = torch.nn.functional.log_softmax (input, dim = 1)
    return  -(target * logprobs).mean()



#training and Evaluation
#Get parameters, start training model
DEVICE     = "cuda" if torch.cuda.is_available() else "cpu"
EPOCHS     = 10
lr         = 1e-3
model      = T_LEAP()
criterion  = torch.nn.MSELoss()
optimizer  = torch.optim.Adam(model.parameters(),lr=lr, amsgrad=True)

soft       = torch.nn.Softmax(dim=1)
# scheduler = StepLR(optimizer, step_size=5, gamma=0.1)


model = model.to(DEVICE)
tr_losses  = [] 
val_losses = []

tr_batch = int(len(train_loader)/train_loader.batch_size)
vl_batch = int(len(valid_loader)/valid_loader.batch_size)

for idx in range(EPOCHS):
  curr_trloss  = 0.0
  curr_valoss  = 0.0
  model.train()
    
  for i,d in enumerate(train_loader):
      
    # Get images, move them to GPU
    image   = d["images"]
    image   = image.permute(0,2,1,3,4).to(DEVICE)
    heatmap = d["heatmaps"]
    heatmap = heatmap.permute(0,4,1,2,3).to(DEVICE)
    

    optimizer.zero_grad()

    output = model(image)
    loss   = softXEnt(output, heatmap)
  
    loss.backward()
    optimizer.step()
    
    curr_trloss += loss.item()
  tr_losses.append(curr_trloss/tr_batch)
    
 
  # Evaluation loop
  model.eval()
  with torch.no_grad():
      for i,d in enumerate(valid_loader):

        # Get images, move them to GPU
        image   = d["images"]
        image   = image.permute(0,2,1,3,4).to(DEVICE)
        heatmap = d["heatmaps"]
        heatmap = heatmap.permute(0,4,1,2,3).to(DEVICE)

        output = model(image)
        loss   = softXEnt(output, heatmap)

        curr_valoss += loss.item()
        # scheduler.step()
          
  val_losses.append(curr_trloss/vl_batch)
    
  # Print losses 
  print(f"Training loss {idx}:",curr_trloss/tr_batch)
  print(f"Validation loss {idx}:",curr_valoss/vl_batch)
  print(" ")
    
print("Training and evalutation is now complete")
#plotloss    
loss_plot(EPOCHS,tr_losses, val_losses)

#save model
state = {
          'epoch': EPOCHS+1,
          'state_dict': model.state_dict(),
          'optimizer': optimizer.state_dict(),
          'learning_rate':lr,
        }
torch.save(state, "cow_model.pth")

My predictions versus ground truth look like:
Prediction

Ground-truth

Mukesh1729 · November 25, 2021, 3:12pm

Hey Frank,

I tried to use the softmax in the last layer with the MSE loss. The model predictions and ground truth look a bit similar to what the prediction was from the last post using the loss function you suggested to me.

Model predictions

They look quite close compared to the target but then I end up with the problem of the loss not going down. The loss you suggested is not helping the model learn the heatmaps somehow but the loss goes down in value. In the ref paper, they mention that softmax was applied as a softmax transformation together with MSE loss. Not sure what that means.
Do you think there might be something that is missing or else I could try? The loss is being compared with the probability of the key points present in each heatmap to the gaussian distribution over a point in a particular location in the confidence/heat map