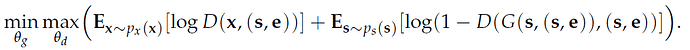I would like to test the architecture from the following paper with a different dataset:
The authors state that their objective function is the following:
Where:
-x is the real grayscale image.
-s is its downsampled version, which should be used both as the initial imput of the generator performing the super-resolution and as a first conditional variable in the learning process.
-e is another two-dimensional array containing values for a second additional conditional variable.
The authors, however, state that this should be implemented by using two separate conditional adversarial losses, one for each of the conditional variables.
To clarify, the first adversarial loss should be:
AdvLoss1(ParametersG, ParametersD) = - Log(Discriminator(x,s) - Log(1-Discriminator(Generator(s),s)
While the second would be:
AdvLoss2(ParametersG, ParametersD) = - Log(Discriminator(x,e) - Log(1-Discriminator(Generator(s),e)
Which should be then summed up for the backward pass.
In my pytorch implementation, however, I have only been able to set up a unique adversarial loss, which could be defined as:
CurrentAdvLoss(ParametersG, ParametersD) = - Log(Discriminator(x,(s,e)) - Log(1-Discriminator(Generator(s),(s,e))
which I calculate in the following training loop (simplified version) as errD and errG after conditioning the network on both s and e at the same time:
for epoch in range(num_epochs):
for i, data in enumerate(trainloader, 0):
############################
# (1) Update D network
###########################
## Train with all-real batch
Discriminator.zero_grad()
s = data[0].to(device)
x = data[1].to(device)
e = data[2].to(device)
x_fake = Generator(s,e)
# Forward pass real batch through D
output_real = Discriminator(x,x_fake,s,e).view(-1)
label_real = torch.ones(len(x), dtype=torch.float, device=device)
# Calculate loss on all-real batch
errD_real = nn.BCELoss(output_real, label_real)
errD_real.backward()
# Train with all-fake batch
x_fake = Generator(s,e)
# Generate fake image batch with G
output_fake = Discriminator(x.detach(), x_fake.detach(),
s.detach(), e.detach()).view(-1)
label_fake = torch.zeros(len(x_fake), dtype=torch.float, device=device)
# Calculate D's loss on the all-fake batch
errD_fake = nn.BCELoss(output_fake, label_fake)
# Calculate the gradients for this batch, accumulated (summed) with previous gradients
errD_fake.backward()
# Compute error of D as sum over the fake and the real batches
errD = errD_real + errD_fake
# Update D
optimizerD.step()
############################
# (2) Update Generator
###########################
Generator.zero_grad()
# Since we just updated D, perform another forward pass of all-fake batch through D
output_fake = Discriminator(x, x_fake,s, e).view(-1)
label_gen = torch.ones(len(x_fake), dtype=torch.float, device=device)
# Calculate G's loss based on this output
errG = nn.BCELoss(output_fake, label_gen)
# Calculate gradients for G
errG.backward()
# Update G
optimizerG.step()
My question is, is there a way to modify the following loop to obtain outputs that have been separately conditioned only first on s and then on e and thus calculate the two separate adversarial losses originally proposed by the authors instead?