Theoretically, a loss function should return 0 when target=prediction, and some positive number when target and prediction and different. In the simple example below, when the prediction=target, I am getting a loss value of -1, and when prediction and target are different, I am getting a loss value of 0. How are these values calculated? What is the intuition behind these values?
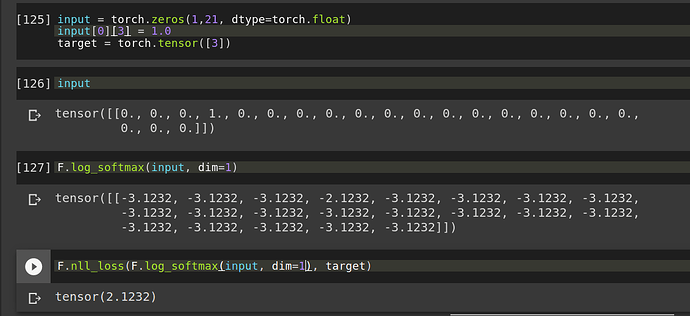
I also tried passing the log_softmax of input, but then also, I am getting a loss value of 2.1232. Again, intuitively, the value of loss in this case should be 0.
What is the intuition/reason behind these loss values?
F.log_softmax expects logits which might have arbitrarily large and small numbers.
If you just call F.softmax on your input tensor, you’ll see that the probability is not exactly one for the desired class:
x = torch.zeros(1, 21)
x[0, 3] = 1.
print(F.softmax(x, 1))
> tensor([[0.0440, 0.0440, 0.0440, 0.1197, 0.0440, 0.0440, 0.0440, 0.0440, 0.0440,
0.0440, 0.0440, 0.0440, 0.0440, 0.0440, 0.0440, 0.0440, 0.0440, 0.0440,
0.0440, 0.0440, 0.0440]])
As you can see, class3 has a probability of 0.1197, so you’ll get a positive loss.
Ahh, got it.
After applying F.nll_loss to this softmax output, I get a loss value of -0.1197 which is close to 0 but not exactly zero. Shouldn’t loss functions return exactly zero when prediction equals target like in this case?
You will get a loss close to zero (in this case you’ll see the print outputs an exact zero, although the value might just underflow), if the logit for the target class is very high:
x = torch.ones(1, 21) * (-10000)
x[0, 3] = 10000
target = torch.tensor([3])
loss = F.nll_loss(F.log_softmax(x, 1), target)
print(loss)
> tensor(0.)
1 Like
Great, understood it! This also forces the network to output larger logit value for the corresponding neuron to reduce the loss during backprop!
Thanks for the explanation