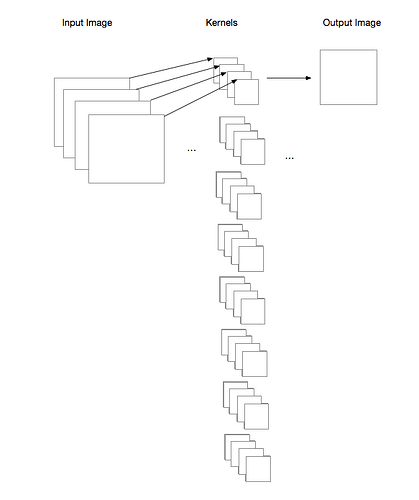
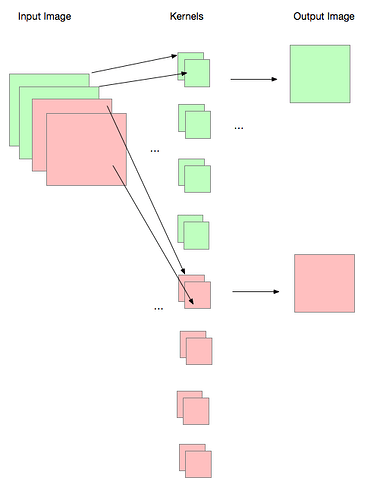
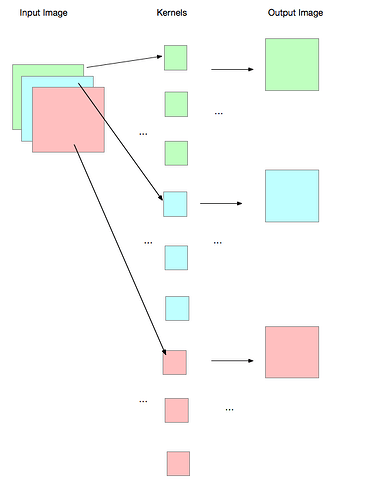
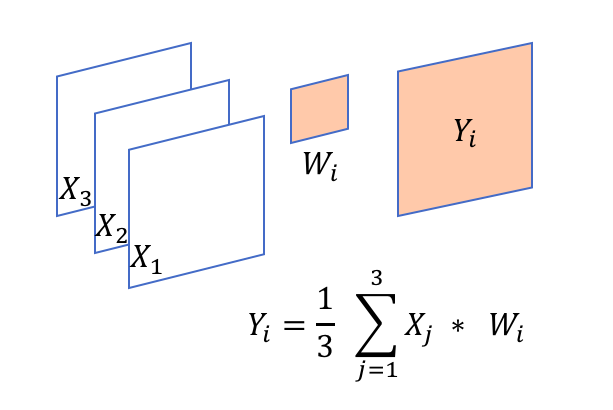
Conv2d certain values for groups and out_channels don't work

vmirly1 · March 1, 2018, 9:48pm

I am playing with the groups option in torch.nn.Conv2d(..). It appears that both in_channels and out_channels must be divisible by groups. But in theory, it is not necessary, for example, if I have in_channels=3, and groups=3, then out_channels=8 should give me the operation shown in the figure, but this will raise an error, saying “out_cnhannels is not divisable by groups”.

This works for in_channels=3, out_channels=9, and groups=3:

>>> conv = torch.nn.Conv2d(in_channels=3, out_channels=9, 
                       kernel_size=(3,3), stride=1, 
                       padding=0, dilation=1, 
                       groups=3, bias=True)

>>> print(conv.weight.data.size())
torch.Size([9, 1, 3, 3])

So, I think out_channels=8 should work as well. Isn’t that right?

Sharing-kernels

rasbt · March 2, 2018, 1:34am

From what I understand, the number of channels in one kernel tensor is equal to the number of channels in the input image. E.g., if you set

c = torch.nn.Conv2d(in_channels=4, out_channels=8, kernel_size=(3, 3), groups=1)

you will have 8 kernel tensors with 4 channels each, corresponding to the following scenario:

Then, if you change it to

c = torch.nn.Conv2d(in_channels=4, out_channels=8, kernel_size=(3, 3), groups=2)

the 8 kernel tensors will be divided such that 2 of them are used for the first 2 image channels, and 2 of them are used for the other 2 image channels. The results are stacked, so if each kernel tensor has 4 channels, you have 2*4=8 output channels and 2 of them will be used for the other 2 image channels.

Now, if you change it to sth like this

c = torch.nn.Conv2d(3, 9, (3, 3), groups=3)

you would end up with 1 kernel channel per image channel:

Finally, if you write sth like you suggested:

c = torch.nn.Conv2d(in_channels=3, out_channels=8, kernel_size=(3, 3), groups=3)

the code will complain, because it wouldn’t now how to evenly distribute the 8 kernels among the 3 input image channels. Eg., the first channel might get 3 kernels, the 2nd gets 3, and the third gets 2? That’s possible but ambiguous.

rasbt · March 2, 2018, 2:14am

@smth
Hm, I was just thinking that it would maybe help to have a parameter called num_kernel_channels_per_input_channels (or probably a shorter name ;)) instead of groups in future? The default could be

num_kernel_channels_per_input_channels = None

which would set num_kernel_channels_per_input_channels equal to the number of channels in the input image. This could make the scenarios above a bit more intuitive and probably more user-friendly.

vmirly1 · March 2, 2018, 2:18am

I see; I thought that each kernel would be shared with all three input channels so given kernel W_k and the 3 input channels X1 X2 and X3, we could have the following:
groups

rasbt · March 2, 2018, 3:21am

Hmm, I don’t think that’s possible in PyTorch without workarounds, but maybe someone else knows more …

Eg as a work around, you could split the input image into 3 matrices, and for each matrix, you could use the same convolutional layer. And then, you could average the results over the three outputs. In pseudo code, sth like this:

x1 = X[:, 0, :, :]
x2 = X[:, 1, :, :]
x3 = X[:, 2, :, :]

o1 = conv2d_1(x1, in_channels=1, out_channels=1...)
o2 = conv2d_1(x2, in_channels=1, out_channels=1...)
o3 = conv2d_1(x3, in_channels=1, out_channels=1...)

o = (o1 + o2 + o3) / 3

smth · March 3, 2018, 1:13am

you can do that by folding the channels dimension into batch dimension, and unfolding after finishing.
For example:

input = Tensor(N, C, H, W)
layer = nn.Conv2d(1, 1, kernel_size)

# first fold C into N
input = input.view(N*C, 1, input.size(2), input.size(3))
out = layer(input)

# unfold
out = out.view(N, C, out.size(2), out.size(3))

michaelklachko · August 16, 2018, 6:37pm

Current docs don’t mention that out_channels should also be divisible by the number of groups:

https://pytorch.org/docs/0.1.12/_modules/torch/nn/functional.html#conv2d

That should be added, IMO.

Jingshuai · May 20, 2019, 10:47am

As I understand and verified, kernel_numbers=out_channels*(in_channels/groups).
For instance, nn.Conv2d(6, 16, kernel_size=(5,5) ,groups=2) makes the learnable parameters of the layer be: torch.Size([16, 3, 5, 5]).

cadip92 · August 13, 2020, 6:28am

You have explained the scenario for a convolution with just 1 output channel. Let’s suppose the no.of input channels are 16 and the no.of output channels are 8 (i.e width multipler = 0.5 as cited in MobileNet paper).
In this case, can I write nn.Conv2d(1,8,3) where 1 is the input channel after folding, 8 are the no.of output channels and 3 is the kernel size ?
Is my understanding correct ?

barto · April 16, 2024, 12:05pm

Sorry for being so late to the discussion but I just had to comment on this as your second example confused me

c = torch.nn.Conv2d(in_channels=4, out_channels=8, kernel_size=(3, 3), groups=2)

so I had to check if my understanding of group convolution was correct. To me it seems that you are saying that each kernel tensor has 4 input channels within each group, and you are also saying that each group only has 2 filters? But clearly if you print out the weight shape you get torch.Size([8, 2, 3, 3]) showing that the input channel is 2, not 4. So my understanding is that in this example there are 2 groups, where each group has 4 filters and each of these 3x3 filter has 2 channels (not 4 channels). So for each group, the filters each take turn on convolving the input (only looking at 2 input channels, one group looks at one half of the input channels and the other group looks at the other half) producing a depth output of 4 because there are 4 filters in a group. Now, since there are 2 groups we will get a total of 8 depth (4+4) on the output, because each group produces 4 depth and therefore stacking them together produces 8 depth.

My understanding comes from this animation at 1:24 where they have 2 groups, and thus has halved the input channels, the output depth is still determined by the number of filters in total (because at the end you just stack the intermediate outputs anyways).

This understanding is consistent even with the third example c = torch.nn.Conv2d(3, 9, (3, 3), groups=3), where the weight shape is shown to be torch.Size([9, 1, 3, 3]). Here we have 3 groups, 3 in_channels and 9 out_channels, so each group will have 9/3=3 filters and each filter will have 3/3=1 in_channel. This means that each group will produce a depth output of 3 because there are 3 filters in a group. But we have 3 groups, so in total when stacking the output we will get a depth of 9 in the end.

And that’s kinda the point of using grouped convolution, by splitting up the computations into groups this effectively reduces the number of input channels on each filter, while still reaping the benefits of the potentially increased output channels in later conv layers to capture richer features. This ultimately reduces the computational cost from O(c_i * c_o) to O(g * c_i/g * c_o/g) = O(c_i * c_o / g), which makes it g times faster, where g is the number of groups, c_i is the input channels and c_o the output channels according to d2l chapter 8.6.5. This also reduces the number of parameters in the same way.