Convolutional Layers with Shared Weights for each Input Channel

1

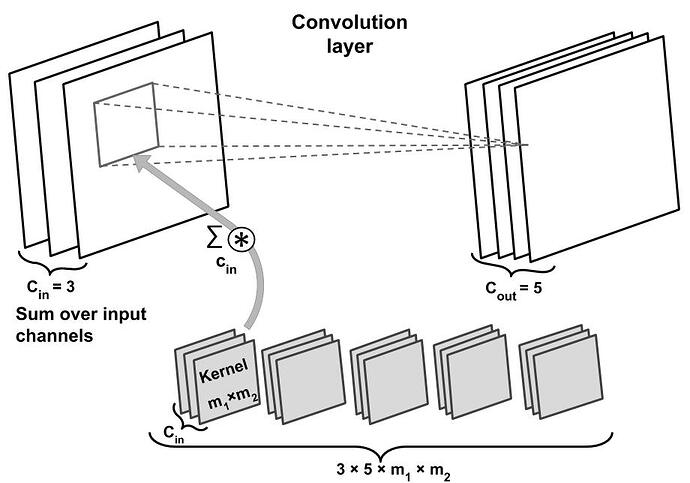
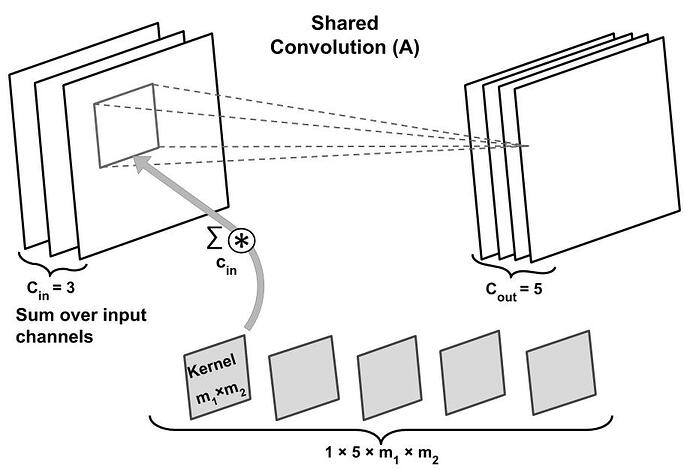
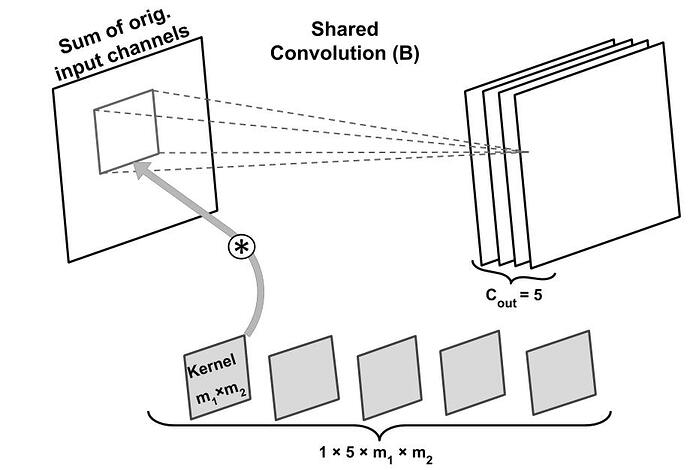
Hello,

What is the right way of implementing a convolutional layer that has shared weights for each input stream?

I have made an implementation where use convolutional layers with a single layer and then loop through each channel of the input stream to apply that convolution.

        z = self.conv0(x[:,0,:].view(x.shape[0], 1, x.shape[2]))
        for i in range(1, x.shape[1]):
            z = torch.cat([z,self.conv0(x[:,i,:].view(x.shape[0], 1, x.shape[2]))], dim = 1)

Another idea that I have was shuffling weights of a convolutional layer but that wouldn’t save from the number of parameters used, although I would expect them to get similar to each other over training.


temp = model.conv1.conv.weight
temp = temp[:,torch.randperm(temp.shape[1]),:]
model.conv1.conv.weight = nn.Parameter(temp)

Finally, I thought the group parameter, which is used for depth-wise separable convolutions, can be used for that purpose, but that’s not the case in the documentation.

I am looking forward for your suggestions. Thank you in advance.

2

One idea is to sum the weights together (or taking their average). The reason is convolution operation has distributivity property: {\displaystyle f*(g+h)=(fg)+(fh)}

So, instead of convolving each input channel with the same filter and then adding them up, I suggest first add the channels together and then apply the convolution.

3

For example, I can show this is true with the following example:

import torch
import torch.nn as nn

conv = nn.Conv2d(1, 8, 3, bias=False) 
x = torch.randn(1, 3, 10, 10) 
y1 = conv(x[:, :1, :, :])
y2 = conv(x[:, 1:2, :, :])
y3 = conv(x[:, 2:, :, :]) 

y = y1 + y2 + y3
print(y[0, 0, :2, :2])

## result: 
tensor([[-0.5882, -0.7958],
        [-0.2555,  1.3778]], grad_fn=<SliceBackward>)

Now, we apply the convolution using the second approach, i.e. first doing the sum over input channels, and then applying the convolution:

x2 = torch.sum(x, dim=1, keepdim=True)
z = conv(x2)
print(z[0, 0, :2, :2])

## result:
tensor([[-0.5882, -0.7958],
        [-0.2555,  1.3778]], grad_fn=<SliceBackward>)

As you can see the result are the same. In fact, the second method is also more efficient, since we do the convolution only one time.

4

Hello, I can’t do that (summing channels) because in the subsequent step I want to keep having the same number of channels as the correlation between those channels are important at later steps.

I thought of averaging the weights instead of shuffling them but then kernels can cancel each other and the mean kernel (of meaningful kernels) might not be meaningful.

5

Well, what you did (using single kernel and then summing them) is not that much different than the one that I have proposed (using single kernel and concatenating the results), which preserved channels.

6

That was just an example. I wanted to show that instead of applying convolution in a loop and then adding them together, you can add the input channels together, and then apply the convolution.

That means you want to define the convolution layer to have the same output channels as the number of input channel. For example if you have 16 input channels, and retaining 16 output channels, then your shared convolution should be : nn.Conv2d(in_channels=1, out_channels=16, kernel_size=3).

7

Yes that’s what I also tried after reshaping the input to have one channel, and reshaping back into 16 channels after having the convolution. But then the number of kernels trained is limited with the output channels. I later developed the concatenating solution as that was not very effective (it was limited).

8

Yes, from what I understood, that was exactly what you were looking for, right? To have shared convolution for each input channel?

9

I would prefer a way that does not changes the general topology of the architecture. I don’t understand why the architecture needs to be changed to re-use the weights for each input channel. In other words, I am looking for a better way to realize this.

10

By the way, this is how I defined the convolutions for the concatenation method. So it actually does kind of what you have suggested finally.

    self.conv0 = base_conv1d(in_channels = 1, out_channels = scaler)
    self.conv1 = base_conv1d(in_channels = in_channels * scaler,  out_channels = 512)
11

So, let’s take a look at what happens in a convolution layer in general. So, given an input X which has shape [c_in, width, height] (ignoring the batch dimension for simplicity), and a filter W which has shape [c_in, c_out, m_1, m_2], then the conv-layer will compute c_in x c_out convolution operations. But the result should still have c_out channels, so it internally sums over the input channels in order to get the one output channel. So this is repeated c_out times, to get c_out channels as output. This is shown in figure below:

conv-layer-1
conv-layer-1920×645 53.9 KB

Now, we want to have a shared convolution layer by which we mean we want the same filter to be applied over all input channels to get one output channel. So, since the filters applied to input channels is the same for each output, then, we can create a filter W_shared which has shape [1, c_out, m_1, m_2]. But note that this is not a valid operaiton now, since th enumber of input channeles and the corresponding channels of filters do not match. So we have to apply the convolution on each input channel individually and the then add the results together. So, this is shown in figure below:

conv-layer-2-shared
conv-layer-2-shared919×626 48.8 KB

Now, the alternative solution to the previous shared convolution is to first add the input channels to reduce its input to 1, and then apply the convolution. This is shown in the following:

conv-layer-3-shared
conv-layer-3-shared919×626 43.9 KB

The last two convolution (shared-convolution-A and shared-convolution-B) yield the same results (assuming that there is no bias).

1 Like
12

Thanks a lot for your effort. I really appreciate it. However, I don’t think that would work for my case. Assume that I am ranking / sorting given images (or another type of dataset). In that case, I would have N inputs and N outputs, and I would need to preserve the knowledge from each channel to the end. (Feature extraction step of those images would preferably be the same, especially at the beginning of the network.

Thus, they would benefit from using same kernels both in terms of sample efficiency, and in terms of memory requirements, etc). To sum up, in this example problem, I can’t just sum the input channels, because if I sum them, the model wouldn’t be able to sort those documents at the final layer as it wouldn’t have any extracted features specific to each document (which are given as input streams). Am I wrong?

13

I have tried also by converting the 1d signal to 2d and then using nn.Conv2d to share the kernels across streams of time series. It worked as I wanted but that somehow consumes huge amount of memory (despite the reduced number of parameters in the model).

14

I don’t understand this part:

Can you please elaborate?

15

Have you understood the ranking example? In order to rank given features at the output layer, a model should be able to know from which stream they have been sourced from. If I take the sum of those streams and then apply convolution, it can’t basically rank them.

16

Okay, but then if you use the same filter across different channels, that will not cause any problem for the ranking?

17

No because that just means that you do same kind of feature extraction.

18

Have you solved this? I met the same question, applying a 1-channel convolutional kernel to different input channels.

19

You can reshape it to move different channels the batch (first) axis and reshape it back once you have the output of that single channel convolution to have multiple channels back. Looping channels and then concatenating the results also works but in that case it is slower I believe since that it is sequential.

1 Like